All in One: Multi-Task Prompting for Graph Neural Networks
预备知识
了解 GNN 领域 graph/edge/node-level 的基本推理模式.
$\mathcal{G} = (\mathcal{V}, \mathcal{E})$, 图;
$\mathcal{V} = \{v_1, v_2, \cdots, v_N\}$ 节点集合;
$\mathbf{x}_i \in \mathbb{R}^{1 \times d}$, 节点 $i$ 的特征;
$\mathcal{E} = \{(v_1, v_j)| v_i, v_j \in \mathcal{V}\}$ 为边集合.
核心思想
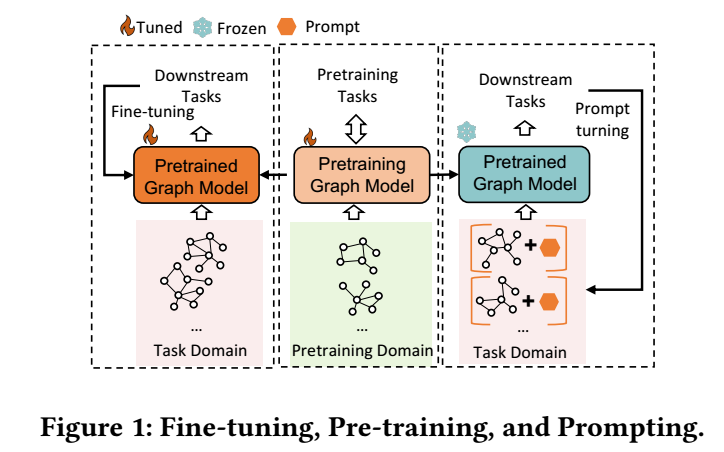
模型的训练主要分为 pre-training 和 fine-tuning 两个阶段, 前者在大量数据集上充分训练得到一个强大的基础模型, 后者在特定任务上微调以追求更加专注的性能.
fine-tuning 又会分为很多种类型, 常见的如所有参数均微调, 或者以 LoRA 为代表的高效微调, 以及本文通过 (soft)-prompt 的 prefix tuning.
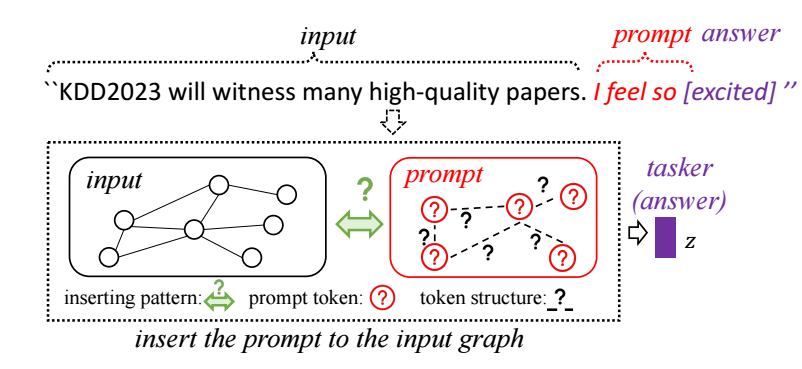
在 NLP 领域, prompt 实际上是一些特殊的 trigger, 能够激发模型做出一些特殊的行为. 如上图所示, ‘I feel so’ 这一 prompt 后面往往会跟随一些表达情感的形容词. 当然, prompt tuning 可以是一些没有字面意义的 prompt 以更灵活地控制模型的输出.
prompt 高效的特点使其大放异彩. Graph 领域的一个特点就是不同任务不同场景下的模型难以直接迁移, 所以本文就希望通过设计 prompt 来实现模型的迁移. 一个最大的问题是如何设计 prompt 能够使得其能够兼容 graph/edge/node-level 的任务.
Reformulating Downstream Tasks
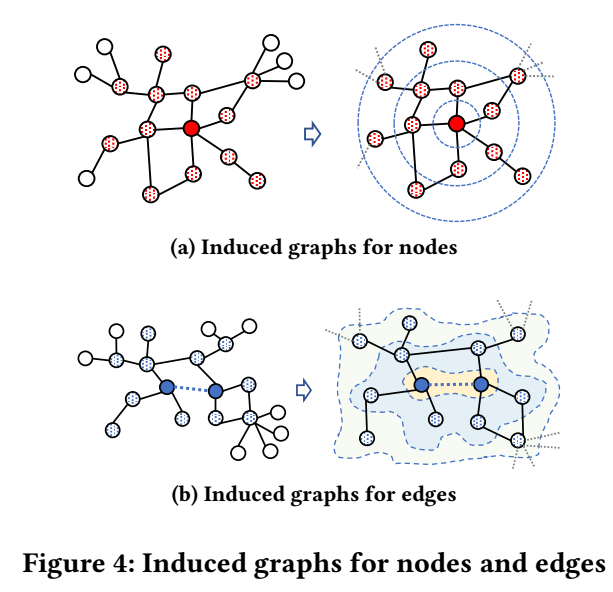
- 作者将三种任务统一为 graph-level 的任务. 对于 node 和 edge 而言, 我们可以将其所对应的 $\tau$-阶子图的图 embedding 作为 node/edge 的表示, 因而可以方便的进行后续的节点分类或者链接预测的任务.
Prompt Graph Design
prompt 的设计是一个难点, 很自然的想法可能是添加一些节点和边, 但是细想下来这种方式往往是 graph-specific 的, 不太具有推广性.
本文将 prompt 设计为一个独立的 prompt graph:
$$ \mathcal{G}_p = (\mathcal{P}, \mathcal{S}), \\ \mathcal{P} = \{p_1, p_2, \cdots, p_{|\mathcal{P}|}\}, \\ \mathcal{S} = \{(p_i, p_j)| p_i, p_j \in \mathcal{P}\}, $$同时每个节点附带一个 token vector $\mathbf{p}_j \in \mathbb{R}^{1 \times d}$.
对于 $\mathcal{S}$ 可以通过如下的方式确定:
- 直接学习边的权重;
- 将 $\mathbf{p}_i \mathbf{p}_j^T$ 作为边的权重.
注: 我没发现 $\mathcal{S}$ 具体用在哪儿了.
然后通过剪枝 (边权重小于一定阈值的置为 0).
通过如下的方式将 prompt graph 注入到原图中:
$$ \hat{\mathbf{x}}_i = \mathbf{x}_i + \sum_{k=1}^{|\mathcal{P}|} w_{ik} \mathbf{p}_k, \\ w_{ik} = \left \{ \begin{array}{ll} \sigma(\mathbf{p}_k \cdot \mathbf{x}_i^T), & \sigma(\mathbf{p}_k \cdot \mathbf{x}_i^T) > \delta, \\ 0, & \text{otherwise}. \end{array} \right . $$