Revisiting Self-attention for Cross-domain Sequential Recommendation
预备知识
(Cross-Domain Recommendation, CDR) 在实际场景中, 一个用户可能在一个平台的不同领域都有一些交互行为, 比如除了在短视频平台上观看视频外, 还在其商城上购买了一些商品等. 显然, 一种天然的假设是用户在不同领域上的行为都能在一定程度上反映用户的行为习惯和偏好, 因此, 我们可能会认为在跨域的数据训练, 最后能够反哺自身, 因而取得更好的性能.
(Cross-Domain Sequential Recommendation, CSDR) 即在序列模型的基础上探讨跨域推荐的可能性. 假设有 domains $\mathcal{D} = \{d_1, d_2, \ldots\}$, 对于每个 domain $d \in \mathcal{D}$, 我们有用户的交互序列
$$ \tag{1} X^d = [x_1^d, x_2^d, x_3^d, \ldots], \quad x_i^d \in \mathcal{V}^d. $$对于跨域推荐而言, 其用户交互序列是不同 domains 的综合结果
$$ \tag{2} X = [x_1, x_2, x_3, \ldots, x_M], \quad x_m \in \mathcal{V} = \cup_d \mathcal{V}^d. $$相对顺序, 通常来说根据发生时间的早晚决定. 因此, 跨域推荐的目标为:
$$ \tag{3} x^* = \underset{x \in \mathcal{V}}{\text{argmax}} \: P(x| X, \{X^d\}_{d \in \mathcal{D}}). $$(Attention) 本文主要关注的是跨域推荐中 Attention 的分布问题, 给定输入 $\mathbf{H}_l \in \mathbb{R}^{M \times r}$, Self-Attention 的计算方式大体如下:
$$ \tag{4} \mathbf{Q} = \mathbf{H}_l \mathbf{W}^Q, \: \mathbf{K} = \mathbf{H}_l \mathbf{W}^K, \: \mathbf{V} = \mathbf{H}_l \mathbf{W}^V, \\ \mathbf{A} = \mathbf{Q} \mathbf{K}^T, \:, \mathbf{H}_{l+1} = \text{softmax}(\mathbf{A}) \mathbf{V}. $$这里我们省略了 Attention Mask, Multi-head Attention 等进阶内容 (与本文关联不大.)
核心思想
在 CDR/CDSR 中, 一个常常遇到的问题是 negative transfer 现象: 引入其他领域的知识反而比不上在 single domain 训练的结果.
因此, 作者认为这个主要是因为在很多情况下, 仅凭借邻域内的交互 $X^d$ 就可以预测准 target 了, 然而跨域序列模型往往在这种情况下分配给其他领域的交互 $X \setminus X^d$ 过大的权重, 导致最终反而预测失败:
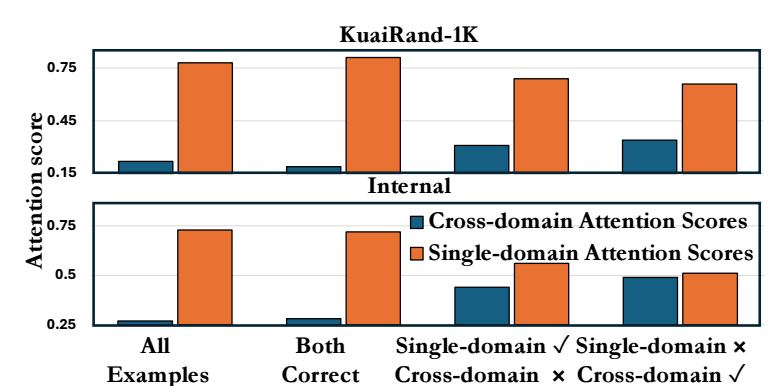
让我们定义 Attention Score $\mathbf{A}$ 在 cross-domain items 上权重的分配比重:
$$ \tag{5} a_{cd} := \sum_{i=1}^M \sum_{j=1} [\text{softmax}(\mathbf{A})]_{ij} \cdot \mathbb{I}[d(x_i) \not = d(x_j)] $$如上图所示: 1) 仅在 single modain 上训练的模型预测失败但是 cross-domain 上预测成功情况为: $a_{cd}$ 呈现一个几乎和 single domain scores 相当的情况; 2) 但是反过来, 仅在 single modain 上训练的模型预测成功但是 cross-domain 上预测**失败*情况也表明了, 跨域训练的模型容易严重高估 cross-domain 的影响, 从而导致 negative transfer.
因此, 作者认为, 我们应该对 Cross-Domain Attention Scores 有一个限制:
$$ \tag{6} \mathcal{L} = \alpha_1 \cdot \ell_{rec} + \alpha_2 \cdot \ell_{cd-attn}, \quad \ell_{cd-attn} = a_{cd}. $$然而, 想要仅仅凭借 loss 来正则化约束 Attention 权重的学习是很难取得最优的性能的. 作者希望借助 Multi-Task/Objective Learning (MTL/MOL) 来帮助实现这一目的, 即
$$ \tag{7} \min_{\theta} \: \underbrace{ \left ( \ell_{rec}(\theta), \ell_{cd-attn}(\theta) \right) }_{\bm{\ell} \in \mathbb{R}_+^2} $$作者主要借助 Pareto MTL 的思想, 首先将 $\mathbb{R}_{+}^2$ 区域划分为 $K + 1$ 个子区域:
$$ \tag{8} \Omega_k = \{\bm{\ell}: \mathbf{p}_k^T \bm{\ell} \ge \mathbf{p}_j^T \bm{\ell}, \: j=0,1,\ldots, K\}, \quad k=0,1,\ldots, K, \\ \mathbf{p}_k = \left(\cos(\frac{k\pi}{2K}), \sin (\frac{k\pi}{2K}) \right) \in \mathbb{R}_+^{2}. $$
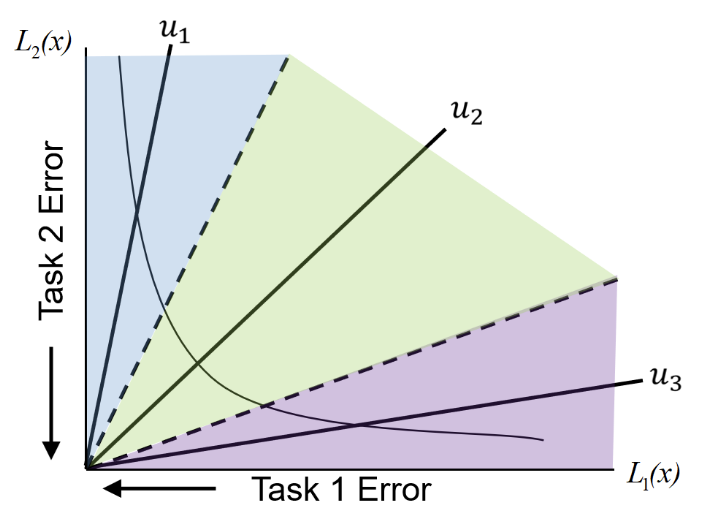
类似上图所示 ($u \rightarrow \mathbf{p}$), 若 $\bm{\ell} \in \Omega_k$, 则表示两个损失的比例和 $\mathbf{p}_k$ 最为接近. AutoCDSR 选择 $\mathbf{p}_1$ 作为理想的区域, 要求最后收敛的损失尽可能满足:
$$ \tag{9} (\mathcal{L}_{rec}, \mathcal{L}_{cd-attn}) \in \Omega_1. $$比如 $K = 5$, 这相当要求 $(\mathcal{L}_{rec}, \mathcal{L}_{cd-attn})$ 尽可能和 $(0.9510565162951535, 0.3090169943749474)$ 保持一致. 总而言之, AutoCSDR 选择 $\mathbf{p}_1$ 反映了对主 loss $\mathcal{L}_{rec}$ 更为重视.
定义违反 (9) 的情况的集合为:
$$ \tag{10} \mathcal{S} = \{\mathbf{p}_k: \mathbf{p}_k^T \bm{\ell} \ge \mathbf{p}_1^T \bm{\ell}\}. $$则, 根据 Pareto MTL, 求解如下问题可以获得一个’最优’的下降方向:
$$ \tag{11} \begin{align*} \min_{\bm{\beta}} \quad & \left \| \sum_{\mathbf{p}_k \in \mathcal{S}} \beta_k \cdot (\mathbf{p}_k - \mathbf{p}_1)^T \nabla_{\theta} \bm{\ell}(\theta) \right \|_2^2, \\ \text{s.t.} \quad & \sum_{\mathbf{p}_k \in \mathcal{S}} \beta_k = 1, \quad \beta_k \ge 0, \: \forall k. \end{align*} $$(11) 可以通过 MGDA 中的 Frank-Wolfe 算法求解. xu需要注意的是, 和 Pareto MTL 中的不同, 这里只对扩展后的 loss 进行了求解.
(AutoCDSR${}^+$) 通过在 Input 引入类似 [CLS] token 的 Information Bottleneck Tokens 来帮助更好地跨域推荐.