Representation Quantization for Collaborative Filtering Augmentation
预备知识
(Collaborative Filtering) 本文考虑通过 User/Item 的特征, 利用双塔模型生成 User/Item 的各自的表示, 用于后续的得分计算.
(Representation Quantization) 作者认为一般的推荐场景面临比较严重的数据稀疏性, 因此希望通过向量量化来得到一些新的特征 (很奇怪的 motivation). 关于向量量化, 请参见 VQ-VAE, RQ-VAE, Product Quantization.
核心思想
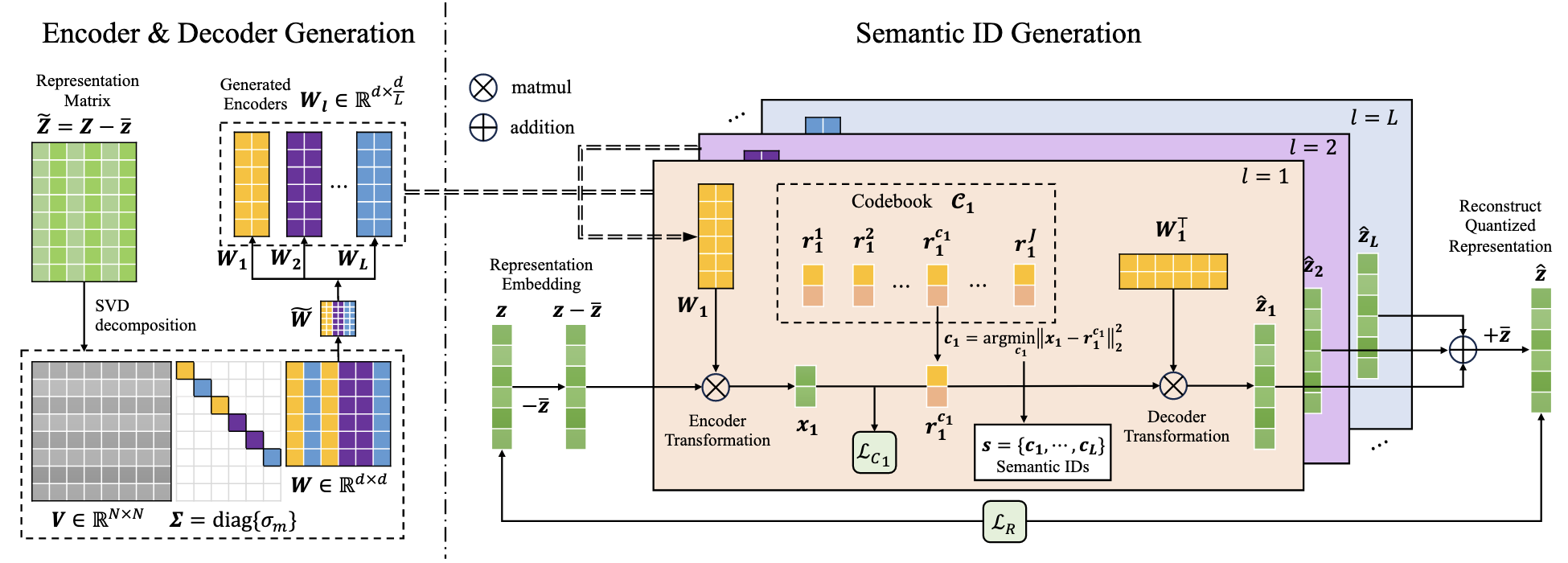
个人觉得本文提出利用正交变换首先对特征维度去相关性, 再进行向量量化的部分挺有意思, 后边应用的部分就略过了.
(SVD) 假设对于 User/Item 我们有特征矩阵 $\bm{Z} \in \mathbb{R}^{N \times d}$ (本文主要针对的是 User), 其中每一行是每个实体的表征 (可以是来自语义编码, 也可以是传统模型预训练得到). 对其进行奇异值分解, 可以得到
$$ \tilde{\bm{Z}} = \bm{V\Sigma W}^T, \\ \tilde{\bm{Z}} = \bm{Z} - \bar{\bm{z}} = \bm{Z} - \frac{1}{N}\sum_{u=1}^N \bm{z}_u, $$其中 $\bm{V} \in \mathbb{R}^{N \times N}, \Sigma \in \mathbb{R}^{N \times d}, \bm{W} \in \mathbb{R}^{d \times d}$.
(切分) 将 $\bm{W}$ 按列重排为 $L$ 个子矩阵:
$$ \tilde{\bm{W}} = [\bm{W}_1, \cdots, \bm{W}_L], \quad \bm{W}_l \in \mathbb{R}^{d \times d/L}. $$重排方式保证, $\bm{W}_l$ 所表示的方差 $\sum_{\bm{w}_m \in \bm{W}_l} \sigma_m^2$ 是差不多的. 这个主要是为了保证每个子空间表达的信息差不多, 最后得到的每个 SID 都有足够的价值.
(DQ-VAE)
Projection: 对于 $\bm{z}$ (行向量), 首先映射到子空间中:
$$ \bm{x}_l = (\bm{z} - \bar{\bm{z}}) \bm{W}_l. $$Quantization: 给定可训练的 CodeBook $\mathcal{C}_l = \{\bm{r}_l^j \in \mathbb{R}^{d / L}\}_{j=1}^J$:
$$ c_l = \text{argmin}_j \|\bm{x}_l - \bm{r}_l^j\|^2. $$Reconstruction: 收集每一个子空间的结果, 可得估计
$$ \hat{\bm{z}} = \sum_{l=1}^L \bm{r}_l^{c_l} \bm{W}_l^T + \bar{\bm{z}}. $$Loss:
$$ \mathcal{L}_T = \mathcal{L}_R + \beta \mathcal{L}_C, \\ \mathcal{L}_R = \|\hat{\bm{z}} - \bm{z}\|_2^2, \quad \mathcal{L}_C = \sum_{l=1}^L \|\bm{x}_l - \bm{r}_l^{c_l}\|_2^2. $$
注1: DQ-VAE 实际上只有 CodeBook 是可训练的, 因此压根不需要 STE 等操作来链接 Encoder-Decoder.
注2: 个人觉得 $\mathcal{L}_R$ 和 $\mathcal{L}_C$ 实际上是等价的. 根据分解的性质, 我们有
$$ (\bm{z} - \bar{\bm{z}}) = \sum_{l=1}^L \bm{x}_l \bm{W}_l^T. $$因此, $\mathcal{L}_R$ 等价于:
$$ \begin{align*} & \|\hat{\bm{z}} - \bm{z}\|_2^2 \\ =& \|\sum_{l=1}^L \bm{r}_l^{c_l} \bm{W}_l^T - \sum_{l=1}^L \bm{x}_l \bm{W}_l^T\|_2^2 \\ =& \|\sum_{l=1}^L (\bm{r}_l^{c_l} - \bm{x}_l) \bm{W}_l^T\|_2^2 \quad \leftarrow \bm{W}_l^T \bm{W}_{l'} = \bm{0}\\ =& \sum_{l=1}^L \|(\bm{r}_l^{c_l} - \bm{x}_l) \bm{W}_l^T\|_2^2 \\ =& \sum_{l=1}^L \|\bm{r}_l^{c_l} - \bm{x}_l\|_2^2 = \mathcal{L}_C \quad \leftarrow \bm{W}_l^T \bm{W}_{l} = \bm{I}\\ \end{align*} $$注3: 所以感觉 DQ-VAE 可能没有训练的必要, 直接子空间的向量拿去做 Product Quantization 应该就行了.