EMR-MERGING: Tuning-Free High-Performance Model Merging
预备知识
了解基本 pretrain-finetune 范式.
预训练模型权重: $W_{pre} \in \mathbb{R}^d$;
微调后的模型权重: $W_i, i=1,2,\ldots, N$.
核心思想
现阶段, pretrain-finetune 最为主流的范式: 即为了推广到一个新的任务上, 我们通常是在一个预训练好的模型上进行微调 (可以是全量微调, 也可以是通过如 分类头, pre-tuning, LORA 等方式进行微调).
现在的问题是, 比如我们可能有许许多多的子任务, 然后我们必须为每个子任务都存一份权重, 即使权重相较于预训练模型的权重会小很多, 这依旧是一个较为麻烦的事情 (其实个人感觉还好, 但是故事是这般讲的).
假设我们有 $N$ 个任务, 分别微调得到了微调后的权重 $W_i, i=1,2,\ldots, N$. 一种很自然的方式是通过平均的方式进行权重融合:
$$ W_M = \mathcal{M}([W_1,\ldots, W_N]). $$
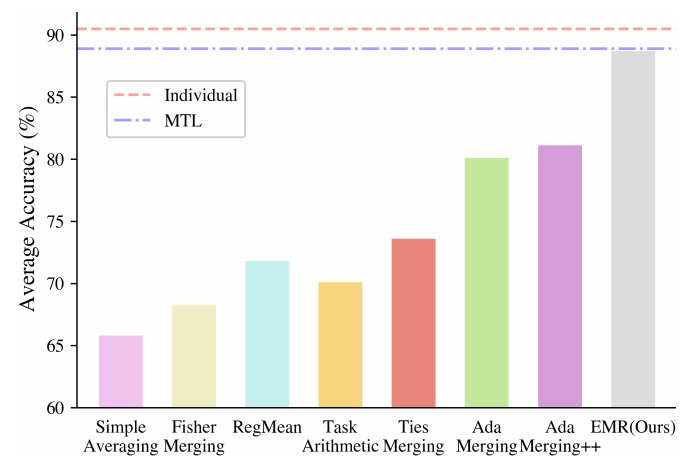
但是如上图所示, 这个结果其实非常糟糕, 当然了, 作者也比较其它的融合方法, 大抵上和单独微调的模型结果相去甚远, 离多任务训练的模型也有不小的差距.
EMR-MERGING 另辟蹊径, 融合之后返回
$$ W_{uni}, [E_1, \ldots, E_N] = \mathcal{M}'([W_1, \ldots, W_N]). $$这里 $W_{uni}$ 是所有任务共享的模型权重, $[E_1, \ldots, E_N]$ 则是每个任务单独的一组参数, 它包含一个非常轻量化的 mask 矩阵以及一个 scale factor. 示意图如下:
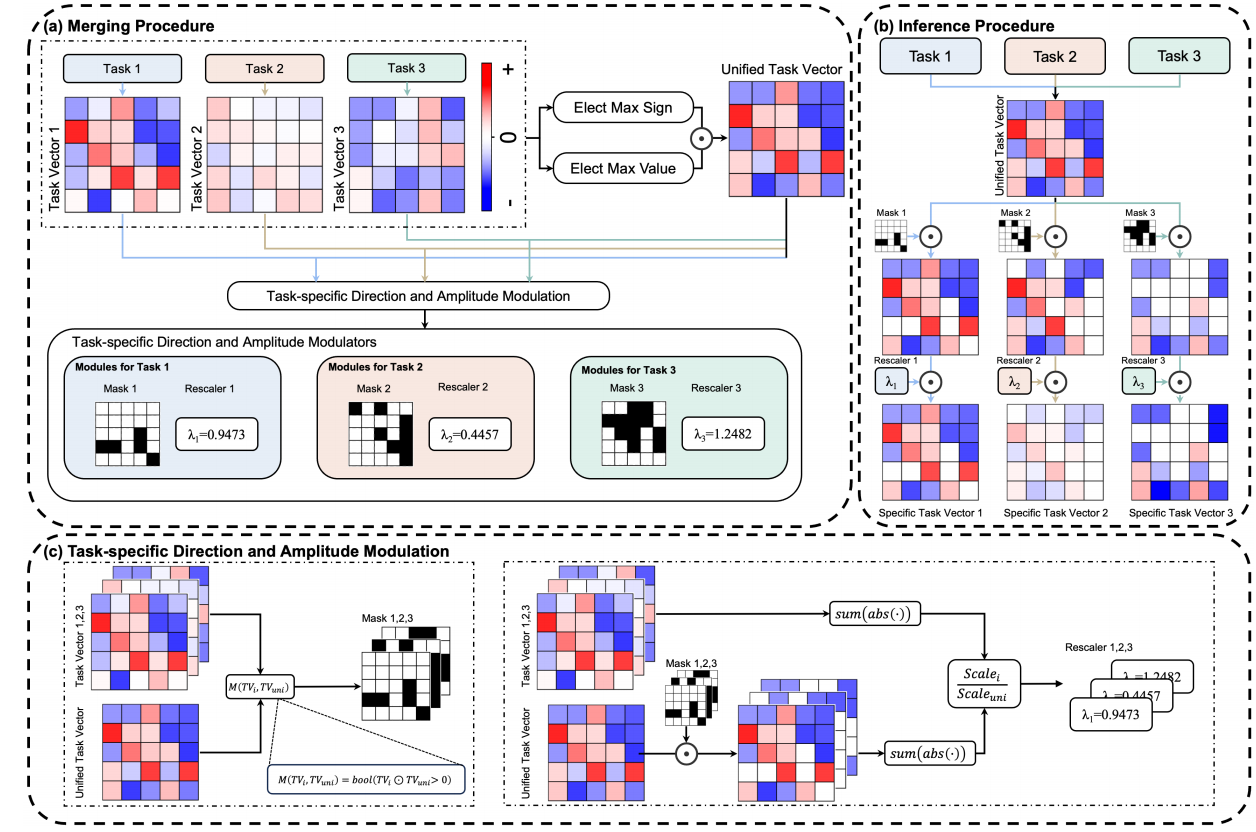
- EMR-MERGING 的具体流程非常简单:
计算每个微调任务的权重 $W_i$ 与预训练权重 $W_{pre}$ 间的差值:
$$ \tau_i = W_i - W_{pre} \in \mathbb{R}^d. $$然后计算:
$$ \tau_{uni} = \gamma_{uni} \odot \epsilon_{uni}, \\ \gamma_{uni} = \text{sgn}(\sum_{i=1}^N \tau_i), \\ [\epsilon_{uni}]_k = \max |[\tau_i]_k| \cdot \mathbb{I}[\text{sgn}([\tau_i]_k) = \text{sgn}([\tau_{uni}]_k)]. $$即 $\tau_{uni}$ 是每个 entry 中和平均结果符号一致的最大值 (in absolute value).
得到了共享的部分之后, 接下来为每个任务 $i$ 计算它所独有的 mask 以及 scale factor:
$$ M_i = (\tau_i \odot \tau_{uni} > 0), \\ \lambda_i = \frac{ \text{sum}(\text{abs}( \tau_i)) }{ \text{sum}(\text{abs}(M_i \odot \tau_F)) }, $$即, 我们只保留和原有权重 $W_i$ 方向一致的, 然后通过一个 scale factor $\lambda_i$ 来使得调整后的权重在 L1 范数上保持不变.
注: 个人其实不太喜欢这个方法, 但是这个问题有一点意思.