Finite Scalar Quantization: VQ-VAE Made Simple

预备知识

• VQ-VAE 提供了一种优雅的向量量化 (离散化表示) 的一种方式, 然而其中的 codebook 的训练以及前置的 encoder 的训练依赖 stop gradient ($\text{sg}(\cdot)$) 以及 straight-through estimator (STE) 操作, 这会导致训练起来比较困难. 具体来说, 可能:

  1. codebook 中的部分向量过于接近, 从而冗余;
  2. 很多向量在训练过程中完全不会匹配到任何向量.

• 习惯上, 我们称训练过程中发生了 Codebook Collapse 的问题.

• 以及有不少文章注意到并且提出了一些解决方案 (包括本文), 我们对部分文章一笔带过:

  1. [1] 中对会对那些长期不产生匹配的向量进行重新初始化;
  2. [2] 主要正对 codebook 的初始化, 不似一般的随机初始化, 其提出根据初始的数据分布, 通过 K-Means++ 进行一个初步的初始化, 并且强调了 scaling 的重要性;
  3. [3] 中提出了一种随机量化的方法, 本质上用 Gumbel-softmax 替代 STE.

核心思想

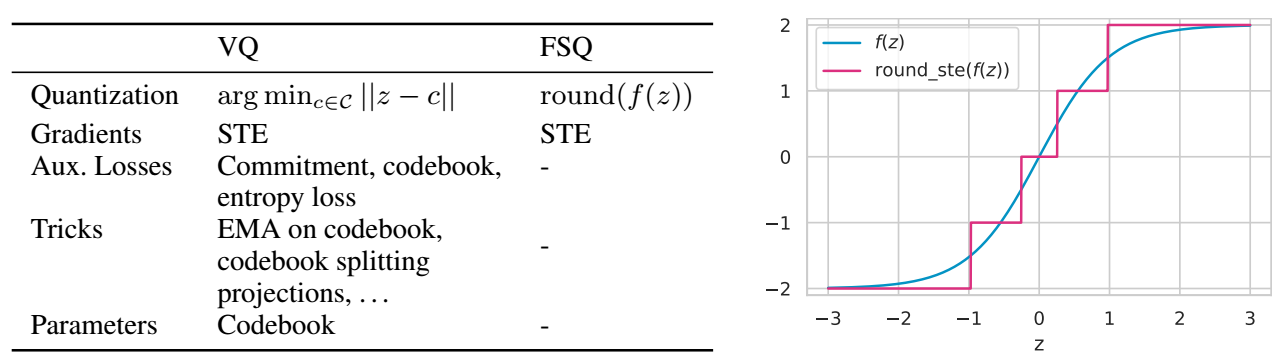
• 注意到, 一般的向量量化 (VQ) 需要一个显式的可训练的 codebook $\mathcal{C} = \{c_k\}_{k=1}^K$, 然后给定一个隐变量 $z \in \mathbb{R}^d$, 通过

  $$ z_q = \text{argmin}_{c \in \mathcal{C}} \|z - c\| $$

  来进行一个量化.

• 本文的不同之处在于, codebook 相当于是预设的好, 无需训练, 其形式为:

  $$ \mathcal{C} = \{-\lfloor L / 2 \rfloor, -\lfloor L / 2 \rfloor + 1, \ldots, 0, \ldots \lfloor L / 2 \rfloor - 1, \lfloor L / 2 \rfloor\}^{d}, $$

  这里 $L$ 是一个超参数, 他直接决定了 CodeBook 的大小:

  $$ |\mathcal{C}| = (2 \lfloor L / 2 \rfloor + 1)^d. $$

• 例子: 当 $L=3, d=3$ 的时候, 我们有

  $$ \mathcal{C} = \{ (-1, -1, -1), (-1, -1, 0), \ldots, (1, 1, 1) \}. $$

• 显然这种不需要训练的 codebook 至少不存在 collapse 中的第一个问题, 实际上它均匀地分布在超立方体之上:

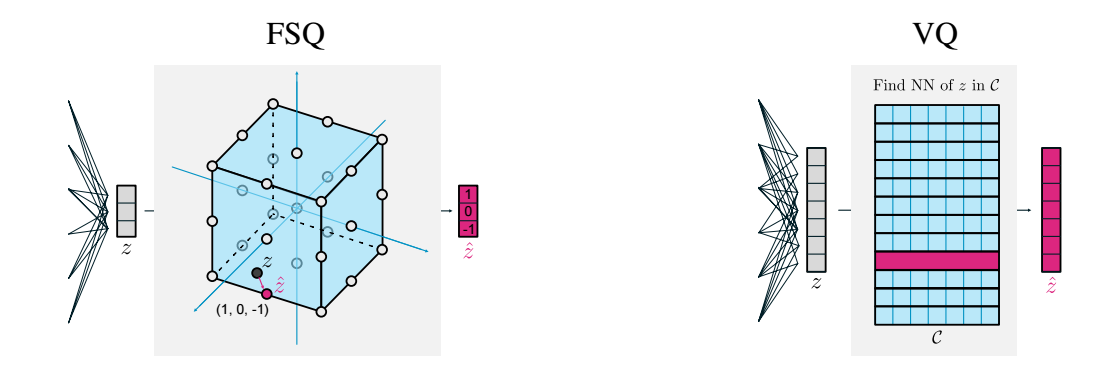
• 当然了, 第二个问题可能还是存在的, 因此 FSQ 还引入了一个 bounfding function $f$, 它将 $z$ 每个元素的值’压缩’到 $[-L/2, L/2]$ 之中去, 比如

  $$ f: z \rightarrow \lfloor L / 2 \rfloor \tanh (z). $$

• 特别地, FSQ 的量化可以以一种非常简便的方式实现, 无需一一计算距离:

  $$ z_q = \text{round}(f(z)). $$

• 其它和普通的 VQ 并没有特别大的区别.

注: $L$ 不一定需要每个维度相同, 可以每个维度单独设置.

参考文献

1. Dhariwal P., Jun H., Payne C., Kim J. W., Radford A. and Sutskever I. Jukebox: A Generative Model for Music. arXiv, 2020. [PDF] [Code]
2. Lancucki A., Chorowski J., Sanchez G., Marxer R., Chen N., Dolfing H. J.G.A., Khurana S., Alumae T. and Laurent A. Robust Training of Vector Quantized Bottleneck Models. arXiv, 2020. [PDF] [Code]
3. Takida Y., Shibuya T., Liao W., Lai C., Ohmura J., Uesaka T., Murata N., Takahashi S., Kumakura T. and Mitsufuji Y. SQ-VAE: Variational Bayes on Discrete Representation with Self-annealed Stochastic Quantization. ICML, 2022. [PDF] [Code]
4. Mentzer F., Minnen D., Agustsson E. and Tschannen M. Finite Scalar Quantization: VQ-VAE Made Simple. arXiv, 2023. [PDF] [Code]