Universal Prompt Tuning for Graph Neural Networks
预备知识
- 了解 GNN 领域 graph/edge/node-level 的基本推理模式.
- $\mathcal{G} = (\mathcal{V}, \mathcal{E})$, graph;
- $\mathcal{V} = \{v_1, v_2, \ldots, v_N\}$, node set, $|\mathcal{V}| = N$;
- $\mathcal{E} \subset \mathcal{V} \times \mathcal{V}$, edge set;
- $\mathbf{X} = \{x_1, x_2, \ldots, x_N\} \in \mathbb{R}^{N \times F}$ 表示 node features.
核心思想
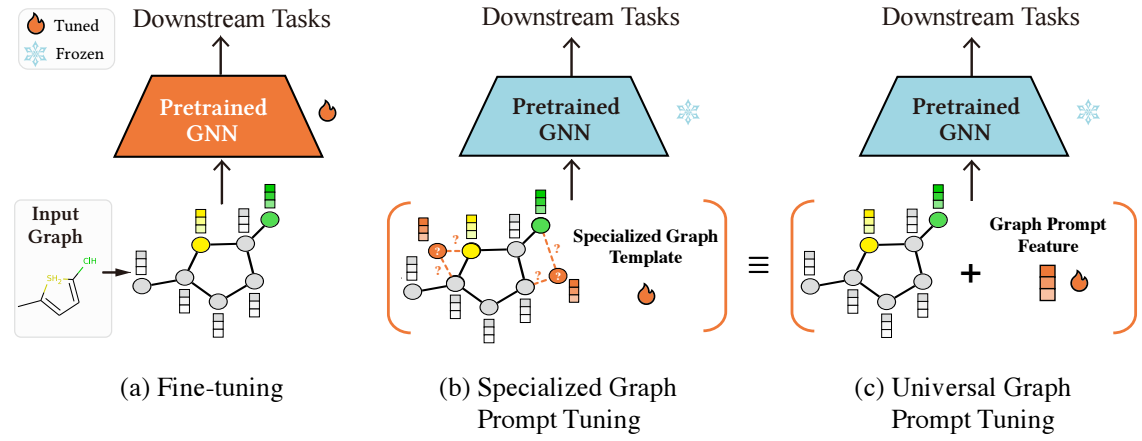
给定预训练好的 GNN 模型, 为了能够应用到不同的下游任务当中去, 我们往往需要进行 fine-tuning. 传统的 fine-tuning 就是对 Pretrained GNN 的参数本身进行一个微调, 但是显然这种方式涉及到相当多的训练参数, 不那么经济实惠.
在 NLP 领域里, 通过 prompt 来激活 base model 在下游任务上的能力已经是被广泛认可且高效的方法. NLP 中, prompt 可以是一些已有的提示词, 如 “xxx, I feel ____” 可以激活模型在情感分析上的一些能力, 这种手段甚至不需要真正的参数微调. 也有一些没有实际含义的 prompt, 即额外插入一些可训练的 token embeddings, 作为 trigger 来激活模型某些特殊的能力. 当然这部分 prompt 需要配合少量的数据进行微调, 但是相较于 (a) 中的全量微调已是相当经济实惠了.
已有一些 GNN 领域的方法试图把这种方法扩展到图领域, 然后以前的方法往往需要针对不同的图结构设计不同的 prompt 模板, 相当不优雅的方案.
本文在经验和理论上证明, 以往的这些 graph prompt 在表达能力上其实等价于直接在图的节点特征上加上一个共享的向量, 即
$$ \mathbf{X} = \{x_1, x_2, \ldots, x_N\} \longrightarrow \mathbf{X} = \{x_1 + p, x_2 + p, \ldots, x_N + p\}, $$这里 $p \in \mathbb{R}^F$ 即可训练的 graph prompt.
作者称上面的方法为 Graph Prompt Feature (GPF), 同时提出另外一种 GPF-Plus:
$$ \mathbf{X} = \{x_1, x_2, \ldots, x_N\} \longrightarrow \mathbf{X} = \{x_1 + p_1, x_2 + p_2, \ldots, x_N + p_N\}, \\ p_i = \sum_{j=1}^k \alpha_{i, j} p_j^b, \quad \alpha_{i,j} = \frac{ \exp(a_j^T x_i) }{ \sum_{l}^k \exp(a_l^T x_i) }. $$这里 $p_1^b, p_2^b, \ldots, p_k^b \in \mathbb{R}^F$ 为 $k$ 个可训练的 prompt 向量.
理论部分请感兴趣的回看原文.