GRAND: Graph Neural Diffusion
预备知识
(Graph) 令 $\mathcal{G} = (\mathcal{V}, \mathcal{E})$ 表示一无向图, 其 nodes $|\mathcal{V}| = n$ 和 edges $|\mathcal{E}| = e$.
(Graph Convolution) 给定节点特征 $\mathbf{x} \in \mathbb{R}^{n}$ (容易拓展到多维的情况 $\mathbf{X} \in \mathbb{R}^{n \times d}$), 图卷积为:
$$ \mathbf{A} \mathbf{x}\: \quad [\mathbf{Ax}]_i = \sum_{j: (i, j) \in \mathcal{E}} a_{ij} x_j. $$这里 $\mathbf{A} = [a_{ij}] \in \mathbb{R}^{n \times n}$ 是图上的权重矩阵, $a_{ij}$ 可以是一些预定义的权重, 也可以是通过特征计算得到的, 如 $a_{ij} = a(x_i, x_j)$.
(Heat Equation) 热扩散方程是基于傅里叶定律推得的微分方程: 热量流动的方向与温度降低的方向相同,其速率与温度的梯度成正比. 令 $u(x, y, z, t)$ 表示时刻 $t$ 时在空间坐标 $(x, y, z)$ 上的温度, 则 Heat Equation 方程为:
$$ \dot{u} = \alpha \cdot \nabla^2 u, $$这里 $\alpha$ 表示一些物理系数, $\nabla^2 u = \frac{\partial^2 u}{\partial x^2} + \frac{\partial^2 u}{\partial y^2} + \frac{\partial^2 u}{\partial z^2}$ 表示 Laplacian 算子. 它实际上刻画了 $(x, y, z)$ 很小的范围内的温度差.
(Graph Diffusion Equation) 在图上, 并不存在连续的空间坐标, 但是有着类似的概念, 对于点 $i$, 它的一阶领居就是 $\mathcal{N}(i) := \{j: (i, j) \in \mathcal{E}\}$ 是一个值得关注的范围. Graph Laplacian 实际上就是刻画 $x_i$ 和它周围邻居 $x_j, j \in \mathcal{N}(i)$ 的差异性. 由此, 我们实际上可以推导出相应的图扩散方程:
$$ \dot{\mathbf{x}}(t) = \underbrace{(\mathbf{A}(\mathbf{x}(t)) - \mathbf{I})}_{\mathbf{\bar{A}}} \mathbf{x}(t). $$这里我们假设 $\mathbf{A}(\mathbf{x}(t))$ 已经是行归一化了, 即 $\sum_{j} a_{ij} = 1$. 实际上, 容易发现, 此时
$$ \dot{x}_i(t) = \sum_{j} a_{ij}x_j - x_i. $$即 $x_i(t)$ 的变化速度正比于 “周围领居的’平均’和自身的差异”, 倘若周围的结点都比我大, 那么他们会给予我更多能量, 于是扩散的结果会让自身增加, 反之减少.
注: 通常来说, Graph Laplacian 定义为
$$ \mathbf{I} - \mathbf{A}, $$因此实际上和一般的 $\nabla^2$ 上有个 ‘$-$’ 的差异, DeepSeek 说 Graph 领域这么做主要是为了保证 Laplacian 矩阵的半正定性. 毕竟除开 Diffusion Equation 外, 我们更习惯分析 Laplacian 的频谱特性, 因此半正定性质会更重要一点.
核心思想
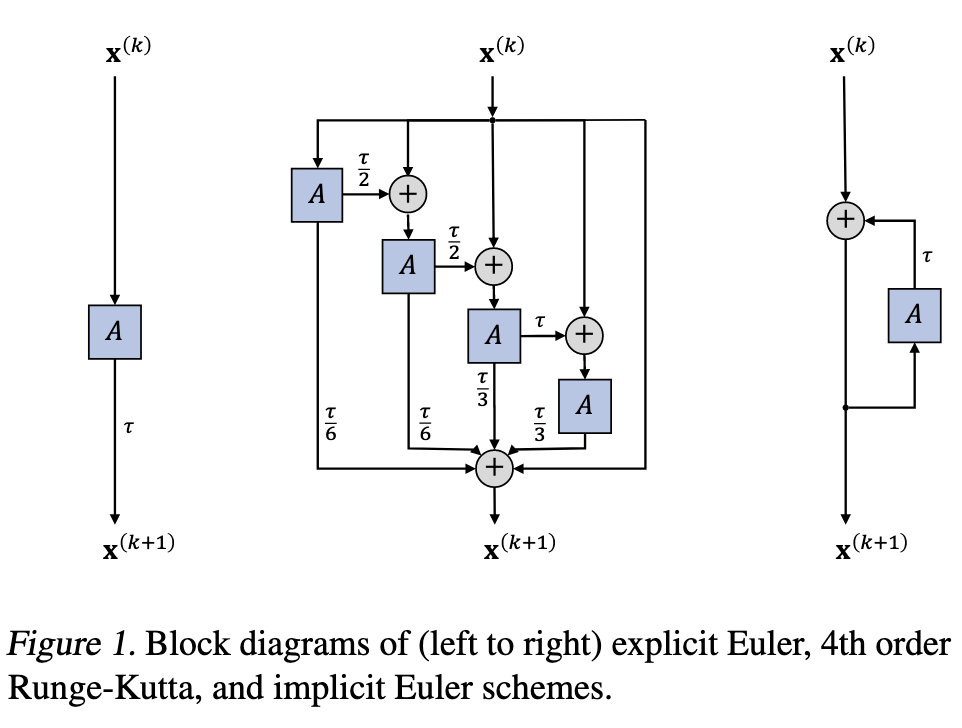
(Graph Diffusion Equation 的离散近似) 图扩散方程为我们提供了一种理解和统一图卷积网络的工具, 通过不同的差分可以得到不同的卷积形式, 作者首先讨论了两种最简单的:
Forward:
$$ \mathbf{x}_{k+1} = \mathbf{x}_k + \tau \cdot \mathbf{\bar{A}}(\mathbf{x}_k) \mathbf{x}_k. $$这里 $\tau$ 表示步长, 实际上就是一步的 Euler 迭代.
Backward:
$$ \mathbf{x}_{k+1} = \mathbf{x}_k + \tau \cdot \mathbf{\bar{A}}(\mathbf{x}_k) \mathbf{x}_{k + 1} \Rightarrow \left( \mathbf{I} - \tau \mathbf{\bar{A}} \right) \mathbf{x}_{k+1} = \mathbf{x}_k. $$相较于 Forward, Backward 需要求解一个线性方程, 因此往往更加耗时.
作者证明, forward 的方式需要保证 $\tau \in (0, 1)$, 而 Backward 则不需要对 $\tau$ 有明显的限制以保证稳定性 (这里稳定性是指近似解的误差对初始值的敏感程度, 越低越稳定). 但是, 实际测试下来, forward 仅在 $\tau=0.005$ 的情况下观测到了还不错的情况.
进一步地, 作者建议采取多步近似策略 (e.g., Runge-Kutta), 或者 Adaptive step size 来取得精度和效率上的最佳.
(GRAND) 本文由此提出了 GRAND:
输入特征 $\mathbf{X}_{in}$ 经过 Encoder 得到初始值:
$$ \mathbf{X}(0) = \phi (\mathbf{X}_{in}). $$初始值经过离散的图扩散得到:
$$ \mathbf{X}(T) = \mathbf{X}(0) + \int_{0}^T \mathbf{\bar{A}}(\mathbf{X}(t)) \mathbf{X}(t) dt. $$通过 Decoder 得到最终的输出:
$$ \mathbf{Y} = \psi (\mathbf{X}(T)), $$其可以用于结点分类预测等任务.
GRAND $\mathbf{A}(\mathbf{X}(t))$ 通过 Scaled Dot Product Attention 得到:
$$ a(\mathbf{X}_i, \mathbf{X}_j) = \text{softmax}( \frac{(\mathbf{W}_K \mathbf{X}_i)^T (\mathbf{W}_Q \mathbf{X}_j)}{d_k} ). $$
Q: 为什么是 $d_k$ 不是 $\sqrt{d_k}$ ?
需要注意的是, 这里也有两种方式:
- (GRAND-l) $\mathbf{A}(\mathbf{X}(t)) \equiv \mathbf{A}(\mathbf{X}(0))$, 即只在扩散前算一次 Attention;
- (GRAND-nl) $\mathbf{A}(\mathbf{X}(t))$, 即每次迭代都重新算 Attention.
根据实验结果, GRAND-l 明显优于 GRAND-nl.
另外, 作者建议可以通过 attention weight 来剔除一些边, 称之为 rewiring.