Dynamic Chunking for End-to-End Hierarchical Sequence Modeling
预备知识
核心思想
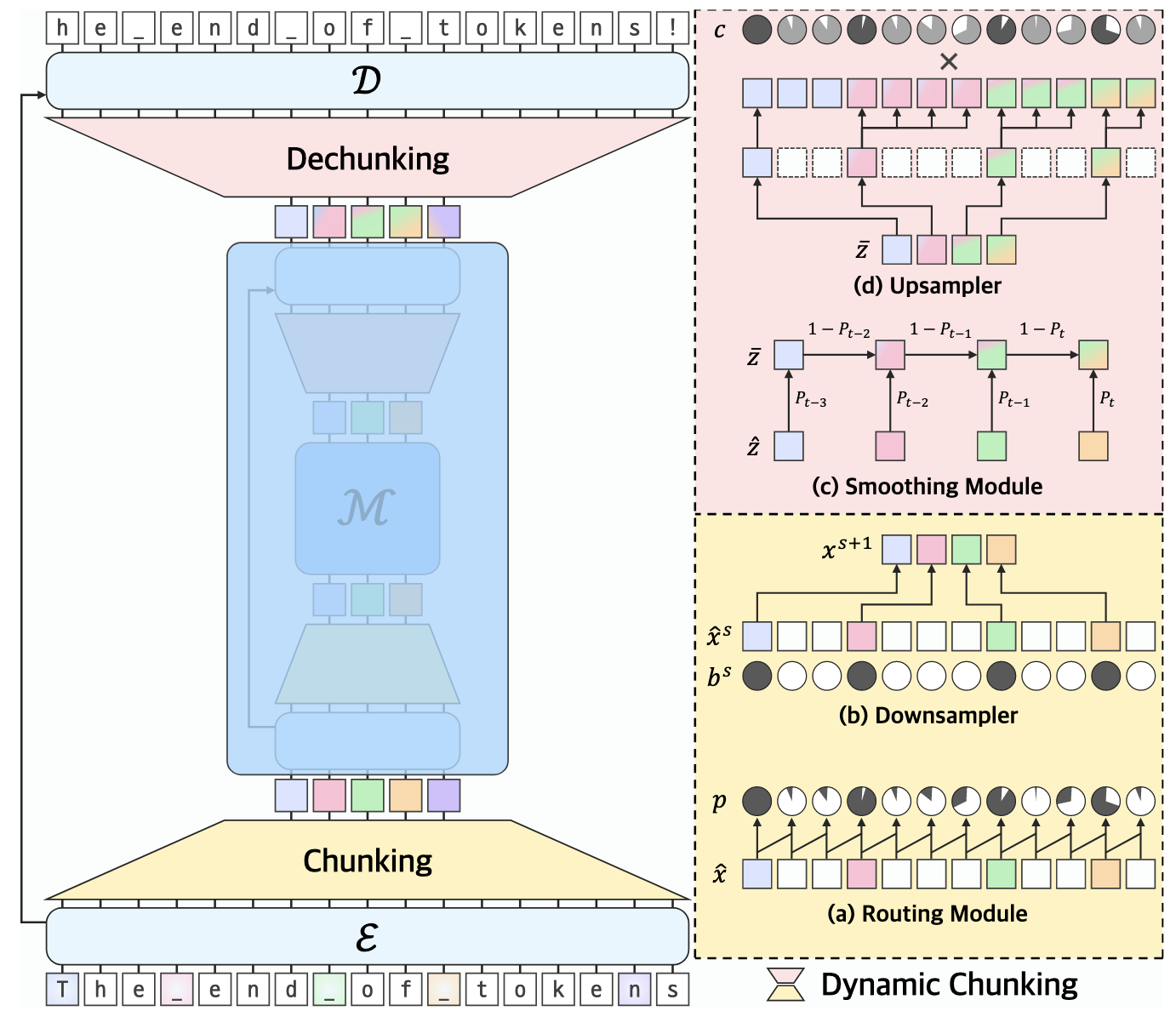
本文的目标是设计一个网络, 不需要 subword tokenizer (e.g., BPE) 也能处理各类序列信息. 换言之, H-Net 可以:
- 直接以 [‘I’, ‘a’, ’m’, ‘M’, ‘T’, ‘a’, ’n’, ’d’, ‘H’, ‘J’, ‘.’] 的符号序列的形式处理自然语言 (因为不受限于 tokenizer, 因此有望对于不同的符号系统有着更好的支持).
- 也可以直接处理图片的 [0-255] 的信号.
MegaByte 和 SpaceByte 在这方面已经做出了很大的贡献, 他们的核心思路其实是将 Byte 通过某种方式切成一个一个 patch, 然后 patch 充当一般的 tokenizer 中的 token 的角色, 用于后续的 Transformer/Mamba 之类模型的推理.
作者认为, MegaByte 的固定 Size 的 Patch 切分策略以及 SpaceByte 的 word-level 的 Patch 切分策略各有缺陷. 前者直接丧失了平移不变性且切分方式缺乏可解释性, 后者显然无法扩展到一般信号中去.
H-Net, 如上图所示, 则会自适应地对符号序列进行一个划分. 特别地, 给定序列 $\bm{x}_1, \bm{x}_2, \ldots, \bm{x}_{t-1}, \bm{x}_t, \ldots \in \mathbb{R}^{d}$, 我们希望找到 patch 和 patch 之间的边界, 作法是每一个都进行一个预测:
$$ b_t = \mathbb{I}[p_t \ge 0.5], \\ p_t = \frac{1}{2}\left[ 1 - \frac{\bm{q}_t^T \bm{k}_{t-1}}{\|\bm{q}_t\| \|\bm{k}_{t-1}\|} \right], \\ \bm{q}_t = W_q \bm{x}_t, \bm{k}_t = W_k \bm{x}_t. $$$b_t = 1$ 表示第 $t$ 个位置是个边界. 显然, 某个位置是边界, 当它和前面的 ’token’ 表示在方向上 (cosine 相似度) 没有啥直接联系. 即, 每个边界可以认为是一个新的 word 的起始.
反复进行上述的动态 Chunking 过程, 即可保证相似的符号聚在一起, 因而序列长度能够大大缩短. 在解码的最后, 需要通过上采样恢复出来. 特别地, 如何保证上采样的梯度可传播性, 训练稳定性, 这里就不多赘述了 (主要是 H-Net 当前版本的符号实在是错误太多).