Temporal Cross-Effects in Knowledge Tracing
预备知识
- 请先了解 DKT 和 Hawkes Process$^{\text{[2]}}$.
核心思想
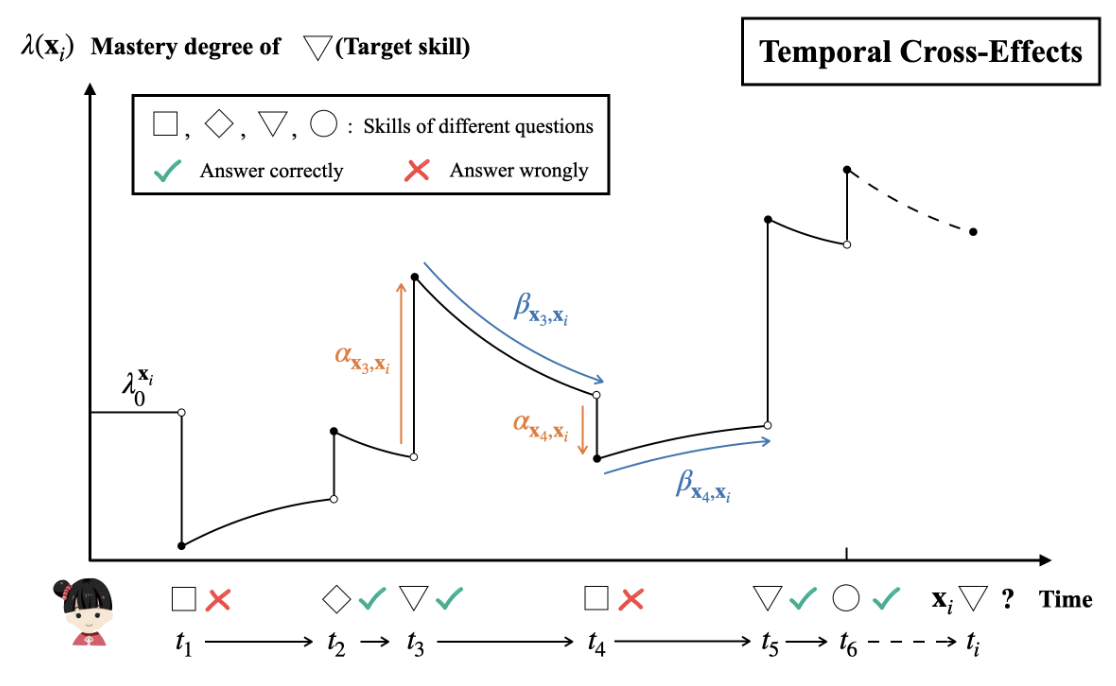
本文希望借助 Hawkes Process 的密度函数来建模:
- 学生掌握技能随着时间的衰减;
- 在知道学生做对做错某类题目后各技能掌握情况的变化.
Hawkes process 的密度函数形如:
$$ \tag{1} \lambda(t) = \lambda_0 + \alpha \sum_{t_j < t} \kappa (t - t_j). $$这里 $t_j, j=1,2,\ldots$ 是已经观测到的事件发生的时间, 而 Hawkes process 的密度函数则是刻画在观测到这些事件发生时间的前提下, 后续发生时间的概率密度分布变化. 一般来说, kernel $\kappa(\cdot)$ 通常是关于 $|t - t_j|$ 单调递减的一个函数, 换言之: Hawkes process 观测到事件发生后, 后续短时间内再次观测到有事件发生的概率是增加的, 反之, 如果长时间没有观测到事件发生, 则往后观测到事件发生的概率是持续下降的.
作者把这种思想融入进了学生的知识掌握状态建模中去, 假设我们观测到学生的作答序列 $\mathbf{x}_0, \mathbf{x}_1, \ldots, \mathbf{x}_{i-1}$ (这里 $\mathbf{x}_i = (q_i, t_i, a_i)$ 为 (题目, 时间, 做对/做错) 的三元组), 我们要凭此来预测下一次交互 $\mathbf{x}_i$ 的情况. 作者将此序列上的作答情况序列建模为:
$$ \tag{2} \lambda (\mathbf{x}_i) =\underbrace{\lambda_{0}^{\mathbf{x}_i}}_{\text{base}} +\underbrace{\sum_{j < i} \alpha(\mathbf{x}_j, \mathbf{x}_i) \kappa(t_i - t_j; \mathbf{x}_j, \mathbf{x}_i)}_{\text{temporal cross-effects}}. $$基于此密度函数, 做对做错的概率预测为:
$$ \hat{y} = \mathbb{P}(a_i = 1) := \frac{1}{1 + \exp(-\lambda(\mathbf{x}_i))}. $$因此, 密度函数越高, 我们认为做对的概率越大.
Base Intensity. 首先, 做对的概率和题目本身的一些特性有关系 (e.g., 知识点以及难易程度), 因此, 我们首先通过 $\lambda_0^{\mathbf{x}_i}$ 来建模这一特性:
$$ \lambda_0^{\mathbf{x}_i} := \lambda_0^{q_i} + \lambda_0^{s(q_i)}. $$这里, $\lambda_0^{q_i}$ 刻画题目本身的信息, $\lambda_0^{s(q_i)}$ 刻画题目所涉及的知识点.
Temporal cross-effects: 我们用 $\alpha(\mathbf{x}_j, \mathbf{x}_i)$ 来刻画题目 $j$ 对 $i$ 的影响, 特别地, 这里只考虑 $(s(q_j), a_j)$ 对于 $s(q_i)$ 的影响. 即, 知识点 $s(q_j)$ 做对 ($a_j = 1$) 或者做错 ($a_j = 0$) 对于判断该学生掌握知识点 $s(q_i)$ 的影响程度. 例如, “加减法"往往是"混合运算"的前置技能, 此时"加减法"如果做错理应降低"混合运算"做对的概率, 反之"混合运算"做对以"加减法"掌握不错为前提, 应当增加"加减法"知识点题目的做对的概率. 另外, 用 $\kappa (\cdot)$ 来刻画时间的衰减:
$$ \kappa(t_i - t_j; \mathbf{x}_j, \mathbf{x_i}) = \exp \left( -(1 + \beta_{\mathbf{x}_j, \mathbf{x}_i}) \log (t_i - t_j) \right). $$这里通过 $\beta$ 实现自适应的衰减. 此外, 用 log-scale $\log (t_i - t_j)$ 而非常规的 $t_i - t_j$ 是因为作者发现作答时间间隔通常是长尾分布的.
$\alpha (\mathbf{x}_j, \mathbf{x}_i):$ 通过如下的方式实现:
$$ \alpha (\mathbf{x}_j, \mathbf{x}_i) = \alpha ((s(q_j), a_j), s(q_i)) = \langle \mathbf{m}_{q_j + a_j |S|}^{\alpha}, \mathbf{n}_{q_i}^{\alpha} \rangle, $$其中 $\mathbf{m}, \mathbf{n} \in \mathbb{R}^d$ 为独立的 embedding.
$\beta_{\mathbf{x}_j, \mathbf{x}_i}:$ 通过如下的方式实现:
$$ \beta_{\mathbf{x}_j, \mathbf{x}_i} = \beta_{(s(q_j), a_j), s(q_i)} = \langle \mathbf{m}_{q_j + a_j |S|}^{\beta}, \mathbf{n}_{q_i}^{\beta} \rangle, $$其中 $\mathbf{m}, \mathbf{n} \in \mathbb{R}^d$ 为独立的 embedding.
通过这种重参数的方式, 可以有效避免由于知识点交互稀疏性所带来的训练不充分问题.
知识点的相互影响: HawkesKT 有一个比较有意思的副产品, 即可以通过 $\alpha$ 来判断两个知识点的影响程度.
注: (2) 并不是一个 Hawkes Process 的密度函数, 因为实际上我们不需要预测学生一下次做题的时间. 作者只是将 Hawkess Process 的衰减特性引入了.