Learnable Item Tokenization for Generative Recommendation
预备知识
- (Generative Recommendation) 生成式推荐依赖对 Item 的标序, 比如常见的用 Title 作为其 identifier 或者利用 RQ-VAE 或者 Residual KMeans 等方式进行向量量化 (由此得到例如 (7, 4, 2) 这类三元组的标识). 然而, 这些方法大都依赖 semantic features, 因此对于 (7, 4, 1) 和 (7, 4, 2) 这两个 Item, 可能仅仅是在语义细节上稍有不同. 然而在推荐系统中, Item-Item 的相似往往不仅仅局限于语义层面, 协同信息往往也非常重要: 即两个被多个相同用户购买的 Item 我们往往也认为是相似的.
核心思想
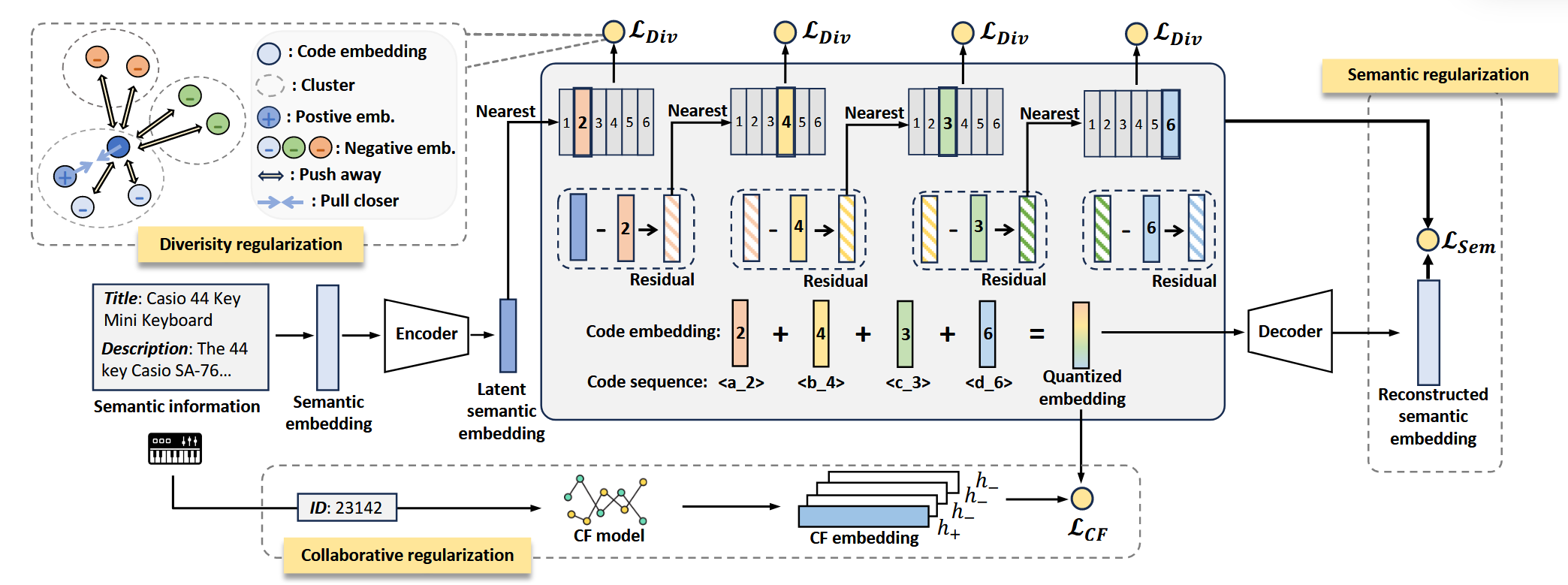
(RQ-VAE) 一般的 RQ-VAE 用于推荐 (见 TIGER) 流程如下:
通过一个 (frozen) 语言模型 (如, t5, llama 等) 得到 Item 的文本表示 $\bm{s}$.
Encoding: 文本表示再通过一个 Encoder 得到中间表示 $\bm{z} \in \mathbb{R}^d$;
Quantization: 然后通过最近邻进行向量量化:
$$ c_l = \text{argmin}_{i} \|\bm{r}_{l-1} - \bm{e}_i\|^2, \quad \bm{e}_i \in \mathcal{C}_l, \\ \bm{r}_l = \bm{r}_{l-1} - \bm{e}_{c_l}, $$这里 $\mathcal{C}_l = \{\bm{e}_i\}_{i=1}^N$ 为第 $l$-level 的 codebook, $\bm{r}_0 = \bm{z}$. 这一步, 我们得到 Item 的一个离散编码 $(c_1, c_2, \ldots, c_L)$.
Decoding: 在训练过程中, 上一步还可以得到一个 $\bm{z}$ 的近似:
$$ \bm{q} = \sum_{l=1}^L \bm{e}_{c_l}. $$其通过一个 Decoder 得到文本表示的近似 $\hat{\bm{s}}$.
训练损失如下:
$$ \mathcal{L}_{\text{Sem}} = \mathcal{L}_{\text{Recon}} + \mathcal{L}_{\text{RQ-VAE}}, \\ \mathcal{L}_{\text{Recon}} = \|\bm{s} - \hat{\bm{s}}\|, \\ \mathcal{L}_{\text{RQ-VAE}} = \sum_{l=1}^L \| \text{sg}[\bm{r}_{l-1}] - \bm{e}_{c_l} \|^2 + \mu \| \bm{r}_{l-1} - \text{sg}[\bm{e}_{c_l}] \|^2. $$
显然, 传统的 RQ-VAE 训练过程都是围绕保留 semantic 信息的, 没有涉及到任何的协同信号.
(Collaborative regularization:) LETTER 的做法也很简单.
通过一个传统的推荐模型, 得到预训练的 Item embeddings $\{\bm{h}\}$, 此为协同信息主导的特征;
然后增加一个对比损失作为约束:
$$ \mathcal{L}_{\text{CF}} = -\frac{1}{B} \sum_{i=1}^B \log \frac{ \exp(\langle \bm{q}_i, \bm{h}_i \rangle) }{ \sum_{i=1}^B \exp(\langle \bm{q}_i, \bm{h}_j \rangle) }. $$
(Diversity regularization:) 此外, 作者为了提高 codebook 的利用率, 增加一个额外的 diversity 的辅助 loss. 具体的, 作者对于每个 codebook 中的向量进行一次 constrained K-means, 然后增加如下的 loss:
$$ \mathcal{L}_{\text{Div}} = -\sum_{i=1}^B \log \frac{ \exp(\langle \bm{e}_{c_l}^i, \bm{e}_+ \rangle) }{ \sum_{j=1, j \not= c_l}^{N} \exp(\langle \bm{e}_{c_l}^i, \bm{e}_j \rangle) }. $$这里 $\bm{e}_+$ 表示同属于同一个 cluster 的任意 code embedding (通过随机采样获得).