Limitations of Dense Retrieval and Beyond
预备知识
(Dense Retrieval/Embedding-based Retrieval) 通过某种方式得到 query $i$ 和 document $j$ 的向量表示 $u_i, v_j \in \mathbb{R}^d$, 然后通过内积计算相似度
$$ \tag{1} s_{ij} = u_i^T v_j, \quad i=1,2,\ldots, m, \: j=1,2,\ldots, n. $$通过 scores $\{s_{ij}\}_{j=1}^n$ 我们可以进行排序, 从而给出 top-$k$ 的一个候选列表. 一个好的检索模型应当尽可能将那些符合 query 的 document 尽可能检索到. 不考虑泛化性的问题, 显然 $d$ 越大, 向量召回的检索能力越强, 那么这个能力和 $d$ 之前有什么具体关系呢?
核心思想
给定 ground-truth relevance matrix $A \in \{0, 1\}^{m \times n}$, 若 document $j$ 符合 query $i$ 则 $A_{ij} = 1$, 否则 $A_{ij} = 0$. 显然通过 (1) 我们能够得到一个近似的关系矩阵
$$ S = UV^T = [s_{ij}] \in \mathbb{R}^{m \times n}, \\ U = [u_i] \in \mathbb{R}^{m \times d}, V = [v_j] \in \mathbb{R}^{n \times d}. $$我们希望通过 $S$ 得到 ranking 和通过 A 得到的类似.
我们首先考虑如下的几种度量 $A$ 复杂的方式:
(row-wise order-preserving rank)
$$ \text{rank}_{\text{rop}} A =\min \{ d| S = U V^T \text{ such that for all } i, j, k, \text{ if } A_{ij} > A_{ik} \text{ then } S_{ij} > S_{ik} \}. $$即我们需要最少的 embedding size $d$ 来保证存在一个 $S$ 和 $A$ 反映相同的 (row-wise) 排序;
(row-wise thresholdable rank)
$$ \text{rank}_{\text{rt}} A =\min \{ d| \exists \{\tau_i\}_{i=1}^m \text{ and } S = U V^T \text{ such that for all } i, j, S_{ij} > \tau_i \text{ if } A_{ij} =1 \text{ and } S_{ij} < \tau_i \text{ if } A_{ij} = 0 \}. $$即我们需要最少的 embedding size $d$ 来保证存在一个 $S$, 它的每一行可以通过一个截断来恢复出 $A$.
(globally thresholdable rank)
$$ \text{rank}_{\text{gt}} A =\min \{ d| \exists \tau \text{ and } S = U V^T \text{ such that for all } i, j, S_{ij} > \tau \text{ if } A_{ij} =1 \text{ and } S_{ij} < \tau \text{ if } A_{ij} = 0 \}. $$即我们需要最少的 embedding size $d$ 来保证存在一个 $S$, 它整体可以通过一个截断来恢复出 $A$.
(关系1) 几个度量之间满足如下关系:
$$ \text{rank}_{\text{rop}} A = \text{rank}_{\text{rt}} A \le \text{rank}_{\text{gt}} A. $$
proof:
由于 $\text{rank}_{\text{gt}} A$ 所关联的集合是 $\text{rank}_{\text{rt}} A$ 集合的一个子集, 因此前者的最小值 $\ge$ 后者的最小值, 因此
$$ \text{rank}_{\text{rt}} A \le \text{rank}_{\text{gt}} A. $$($\text{rank}_{\text{rop}} A \le \text{rank}_{\text{rt}} A$) 对于满足 $\text{rank}_{\text{rt}}A$ 的任意 $S$, 我们有
$$ A_{ij} = 1 \Rightarrow S_{ij} > \tau_i, \\ A_{ij} = 0 \Rightarrow S_{ij} < \tau_i. $$倘若 $A_{ij} > A_{ik}$, 则必定有 $A_{ij} = 1, A_{ik} = 0$, 即
$$ S_{ij} > \tau_i > S_{ik}. $$即 $S$ 一定是在 $\text{rank}_{\text{rop}}$ 意义上近似 $A$ 的矩阵. 因此 $\text{rank}_{\text{rop}} A \le \text{rank}_{\text{rt}} A$.
($\text{rank}_{\text{rop}} A \ge \text{rank}_{\text{rt}} A$) 对于满足 $\text{rank}_{\text{rop}}A$ 的任意 $S$, 我们有
$$ A_{ij} > A_{ik} \Rightarrow S_{ij} > S_{ik}. $$定义集合
$$ \mathcal{M} = \{S_{ij}| A_{ij} = 1\}, \quad \mathcal{N} = \{S_{ij}| A_{ij} = 0\}, $$取 $\tau_i = (\min(\mathcal{M}) + \max(\mathcal{N})) / 2$, 显然有
$$ A_{ij} = 1 \Rightarrow S_{ij} > \tau_i, \\ A_{ij} = 0 \Rightarrow S_{ij} < \tau_i. $$即 $S$ 也一定是在 $\text{rank}_{\text{rt}}$ 意义上近似 $A$ 的矩阵. 因此 $\text{rank}_{\text{rop}} A \ge \text{rank}_{\text{rt}} A$.
(Sign Rank) 对于矩阵 $M \in \{-1, 1\}^{m \times n}$, 定义它的 sign rank 为
$$ \text{rank}_{\pm} M = \min \{ d| S \in \mathbb{R}^{m \times n} \text{ such that for all } i, j \text{ we have sign} S_{ij} = M_{ij} \}. $$(Lower Bound & Upper Bound) 对于二元矩阵 $A$, 我们有如下关系成立:
$$ \text{rank}_{\pm} (2A - \bm{1}_{m \times n}) - 1 \le \text{rank}_{\text{rop}} A = \text{rank}_{\text{rt}} A \le \text{rank}_{\text{gt}} A \le \text{rank}_{\pm} (2A - \bm{1}_{m \times n}). $$
proof:
($\text{rank}_{\text{gt}} A \le \text{rank}_{\pm} (2A - \bm{1}_{m \times n })$) 假设 $S$ 是满足和 $2A - \bm{1}_{m \times n}$ 相同符号的矩阵, 则有
$$ S_{ij} > 0 \Leftrightarrow 2 A_{ij} - 1 > 0 \Leftrightarrow A_{ij} = 1. $$因此, $\tau = 0$ 就是使得 $S$ globally thresholdable 的阈值.
($\text{rank}_{\pm} (2A - \bm{1}_{m \times n }) - 1 \le \text{rank}_{\text{rt}}(A)$) 假设 $S$ 是满足 row-wise thresholdable 的矩阵且其秩恰为 $\text{rank}_{\text{rt}} A$. 此时存在 $\tau_i, i=1,2,\ldots, m$
$$ A_{ij} = 1 \Rightarrow S_{ij} > \tau_i, \\ A_{ij} = 0 \Rightarrow S_{ij} < \tau_i, \\ $$因此 $S - \tau \bm{1}_n^T$ 和 $2A - \bm{1}_{m \times n}$ 有相同的符号. 因此
$$ \text{rank}_{\pm} (2A - \bm{1}_{m \times n}) \le \text{rank}(B - \tau \bm{1}_n^T) \le \text{rank}(B) + \text{rank}(\tau \bm{1}_n^T) = \text{rank}_{\text{rt}} A + 1. $$
- 上面的理论了说明了一个重要问题, 即只有当 $d \approx \text{rank}_{\pm} (2A - \bm{1}_{m \times n})$ 的时候, Dense retrieval 才有足够的能力逼近真实的 $A$. 然而, 总存在 $A$, 其 $\text{rank}_{\pm} (2A - \bm{1}_{m \times n})$ 可以任意大, 即总有一些 case Dense retrieval 难以胜任.
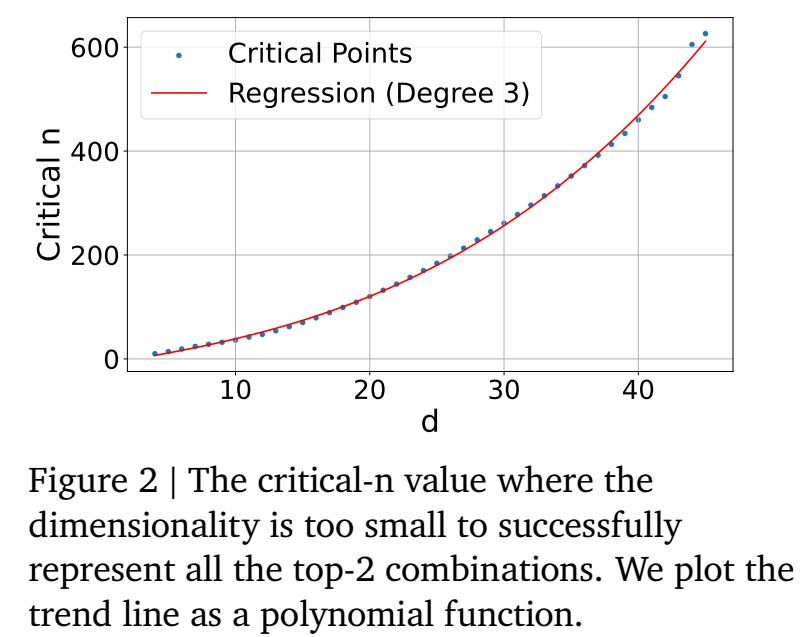
如上图所示, 作者做了一个简单的实验, 在 top-2 组合下, 不同 embedding size 所能检索的范围 $n$. 进一步插值可以得到, 500K 需要 $d \ge 512$, 4M 需要 $d \ge 1024$, 250M 需要 $d \ge 4096$.
注意, 上面用 $S$ 去近似 $A$ 实际上也只是考虑了非常理想的情形:
- 一方面, 在实际中 $A$ 是部分可观测的;
- 另一方面, 由于计算资源受限, 每次实际上我们只能选一部分 $(i, j)$ 用于训练. 在推荐系统中, 负样本的数量起到了决定性作用.
(Generative Retrieval) 那么生成式检索是否能够解决 Dense retrieval 的局限呢? 个人认为, 仅从复杂度的角度来说生成式检索应该不会比 Dense retrieval 有更多优势. 实际上, [2] 中已经部分指出, 生成式检索实际上拟合的是一颗树, 可以通过增加树的状态数量 (即 codewords 的数量) 和树的深度 (即 codebooks 的数量) 来适应庞大的 $n$. 代价是需要更大的模型和更多的推理成本.