Math-Shepherd: Verify and Reinforce LLMs Step-by-step without Human Annotations
预备知识
- 对 Reward Model 有所认知, 看一下 [Let’s Verify Step by Step].
核心思想
Reward Model 有两个重要用途:
- (Training) 用于价值对齐;
- (Inference) 用于打分, 以从多个回答中选择最合适的.
Reward Model 的训练同样有两个主要途径:
Outcome-supervised Reward Model (ORM): 以输出结果作为监督信号:
$$ \mathcal{L}_{ORM} = y_s \log r_s + (1 - y_s) \log (1 - r_s). $$这里 $y_s \in \{0, 1\}$ 是 solution $s$ 的 golden answer (错/对), $r_{s} \in (0, 1)$ 则是 ORM 的打分.
Process-supervised Reward Model (PRM): 以阶段反馈作为监督信号.
$$ \mathcal{L}_{PRM} = \sum_{i=1}^K y_{s_i} \log r_{s_i} + (1 - y_{s_i}) \log (1 - r_{s_i}). $$这里 $y_{s_i} \in \{0, 1\}$ 是 solution $s$ 在 step $i$ 处的 golden answer (错/对), $r_{s_i} \in (0, 1)$ 则是 ORM 的打分.
以做数学题为例, 最简单的训练方式就是以最终的答案作为标准来训练 reward model, 此时就是 ORM. 但是数学题有些时候过程不对但是答案还是可能是对的, 倘若我们要求对于每一个 step 都打分, 此时就是 PRM. 显然:
- ORM 相较于 PRM 会存在 false positives 的问题;
- PRM 相较于 ORM 则需要更多的监督信号, process supervision 往往需要额外的人类打标.
为了解决 PRM 中需要人类打标的问题, 本文提出了 Math-Shepherd, 一种通过频率估计来实现 process supervision.
Estimation
因为我们没有真正的 $y_{s_i}$, 需要通过某种方式估计它. 作者认为, solution $s_i$ 是更可靠的, 如果这个 step 更容易导向正解.
对于一个 reasoning step $s_i$, 我们继续采样 $N$ 个 solutions:
$$ \{(s_{i+1, j}, \cdots, s_{K_j, j}, a_j)\}_{j=1}^N, $$其中 $a_j$ 是第 $j$ 次采样的答案, $K_j$ 是总共的 steps.
据此, 我们可以估计
Hard estimation (HE):
$$ y_{s_i}^{HE} = \left \{ \begin{array}{ll} 1, & \exist a_j, a_j = a^*, \\ 0, & \text{otherwise}. \\ \end{array} \right . $$Soft estimation (SE):
$$ y_{s_i}^{SE} = \frac{\sum_{j=1}^N \mathbb{I}[a_j = a^*]}{N}. $$
通过估计的结果就可以训练 PRM 了, 当然代价就是采样的时间是不菲的.
Verification
采取所有 step 打分的最小值作为整个 solution 的 score;
通过如下方式可以综合 $N$ 个采样得到的 solutions 的结果:
$$ \text{argmax}_{a} \sum_{i=1}^N \mathbb{I}(a_i = a) \cdot PRM(p, S_i), $$这里 $p, S_i$ 分别表示问题 $p$ 的第 $i$ 个 solution.
实验结果
- PRM 用于 verification:
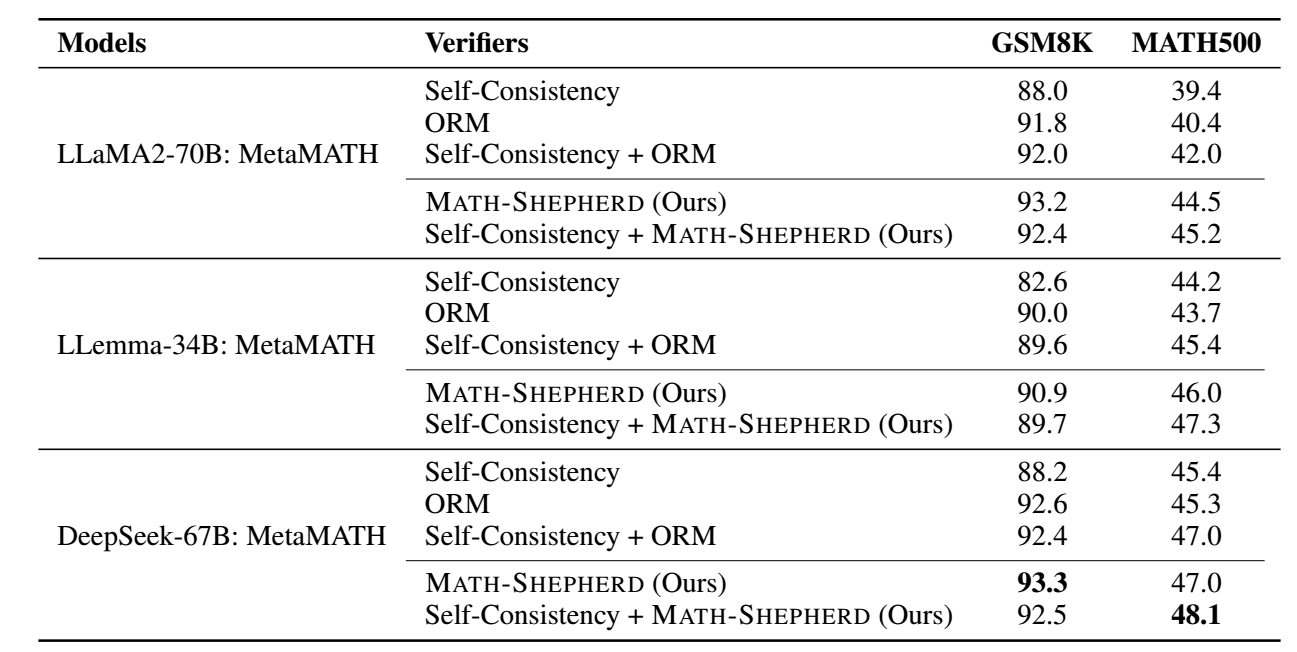
这种情况下, 似乎并没有非常明显的一个效果提升.
PRM 作为 RL reward model:
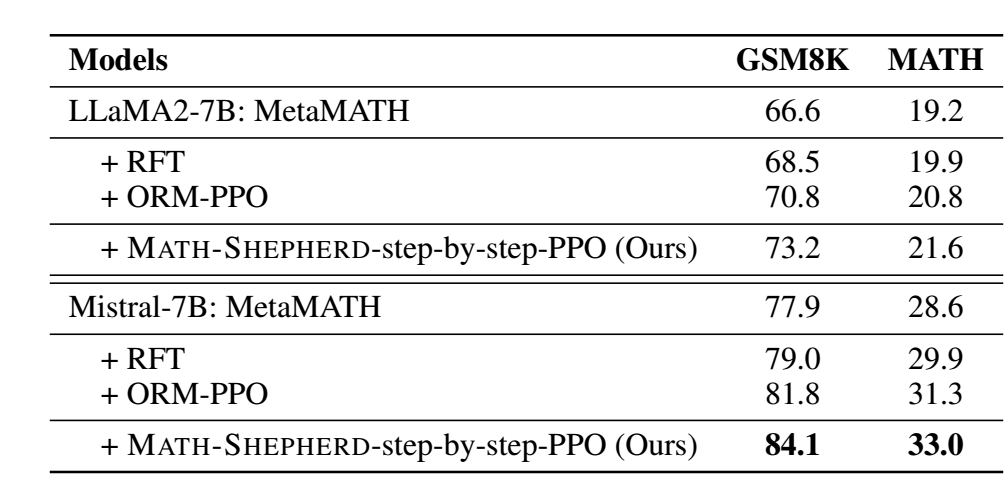
- 似乎比上面的要明显不少.