Round and Round We Go! What makes Rotary Positional Encodings useful?
预备知识
- 需要对 Rotary Positional Encoding (RoPE) 有基本的了解.
感觉是相当不错的实验性文章, 看它的审稿意见, 审稿人主要质疑的点是模型过于局限于 Gemma, 而位置编码过于局限于 RoPE.
核心思想
虽然 Causal Transformer 对于不同位置的 tokens 是具备一定区分性的, 但是为了进一步增强这一点, 位置编码已经成了一个被广泛采用的基本组件了.
令 $\mathbf{x}_i \in \mathbb{R}^d$ 为第 $i$ 个位置上的 token embedding, 其所对应的 query 和 key vectors 为
$$ \mathbf{q}_i = \mathbf{W}_Q \mathbf{x}_i, \quad \mathbf{k}_i = \mathbf{W}_K \mathbf{x}_i \in \mathbb{R}^d. $$假设序列长度为 $n$, 即 $\mathbf{x}_1, \ldots, \mathbf{x}_n$, 则可以通过如下公式计算 $i,j$-th 的 attention:
$$ \alpha_{i, j} = \frac{\exp(\mathbf{a}_{i, j})}{ \sum_{\ell \le i} \exp(\mathbf{a}_{i, \ell}) }, \quad \text{with } \mathbf{a}_{i,j} = \phi(\mathbf{q}_i, \mathbf{k}_j). $$这里我们省略了 $1 / \sqrt{d}$, 并仅讨论 causal attention.
由于相对位置编码的可延展性, 进行这部分增强的 attention 计算过程为 $\mathbf{a}_{i,j} = \phi(\mathbf{q}_i, \mathbf{k}_j, i - j)$.
RoPE
RoPE 是一种可以通过类似绝对位置编码方式实现的相对位置编码, 其本质上是对 $\mathbf{q}_i, \mathbf{k}_i$ 每两个维度独立施加旋转变换:
$$ \underbrace{\left [ \begin{array}{ccccccc} \cos (ig_1) & -\sin (i g_1) & 0 & 0 & \cdots & 0 & 0 \\ \sin (ig_1) & \cos (i g_1) & 0 & 0 & \cdots & 0 & 0 \\ 0 & 0 & \cos (ig_2) & -\sin (i g_2) & \cdots & 0 & 0 \\ 0 & 0 & \sin (ig_2) & \cos (i g_2) & \cdots & 0 & 0 \\ \vdots & \vdots & \vdots & \vdots & \ddots & \vdots & \vdots \\ 0 & 0 & 0 & 0 & \cdots & \cos (ig_{d/2}) & -\sin (i g_{d / 2}) \\ 0 & 0 & 0 & 0 & \cdots & \sin (ig_{d/2}) & \cos (i g_{d / 2}) \\ \end{array} \right ]}_{\mathbf{R}^i} \underbrace{ \left [ \begin{array}{c} q_1 \\ q_2 \\ q_3 \\ q_4 \\ \vdots \\ q_{d-1} \\ q_{d} \\ \end{array} \right ] }_{\mathbf{q}_i}. $$其中 $g_k = \theta^{-2(k-1)d}, k=1, \ldots, d / 2$, $\theta$ 通常取一个较大的数, 比如 $10,000$ 甚至 $500,000$. 容易发现, $g_k$ 代表了对应位置的最小旋转角: (1) 对于 $k=1$, $g_1 = 1$ 这是最大的旋转角, 而对于 $k = d / 2$, $g_{d/2} = \theta^{-(d - 2) / d} \approx \theta^{-1}$, 对于正常的 setting, 其实代表一个非常非常小的旋转角. 仅就旋转角而言, 旋转角越小, 越倾向于低频, 即维度靠后的位置更多的对应低频 (需要注意的是, 这不意味着输入 $\mathbf{x}$ 本身就是从高频到低频信息排列的).
RoPE 的距离衰减
- RoPE 其实提出的一个初衷是希望 $\phi(\mathbf{q}_i, \mathbf{k}_j, i - j)$ 随着 $i - j$ 的增大 (即相对距离的增加) 而逐步衰减.
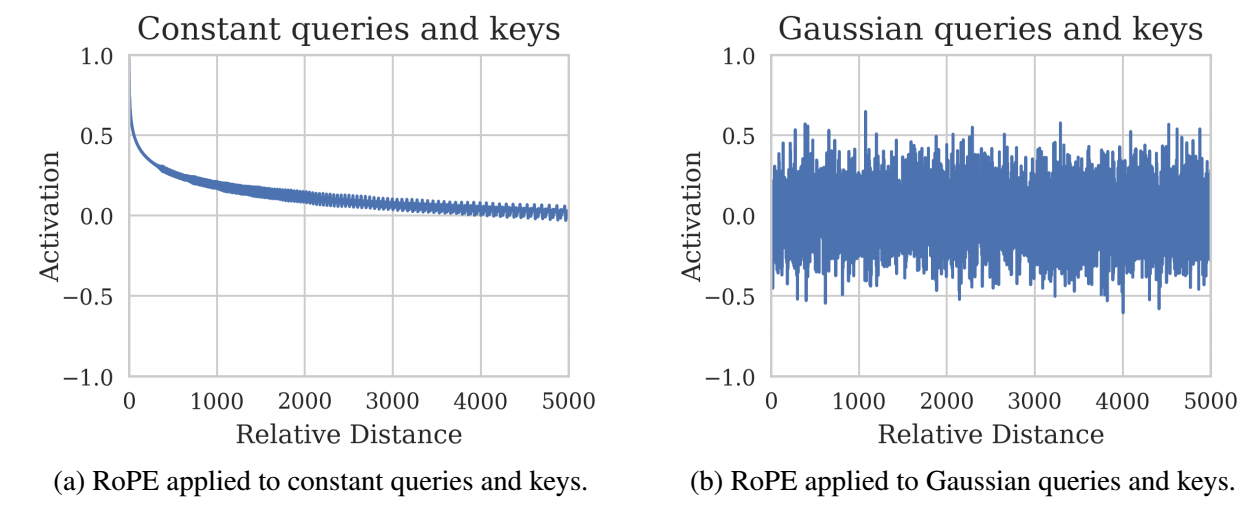
如上的左图即使经常被用来论证这一点, Su 在其博客中实质上给出了 $\mathbf{a}_{i,j}$ 的一个上界, 且同时发现改上界随着相对距离 $i-j$ 的增加是逐步衰减的. 但是, 作者给出论点是这个上界基本上是需要整个 query, key 的所有元素同号才能达成, 在真实情况下这个上界其实相当宽松, 从而导致距离衰减并没有实质性的发生. 实际上, 容易发现:
$$ \mathbf{E}[\phi(\mathbf{R}^i \mathbf{q}_i, \mathbf{R}^j \mathbf{k}_j)] =\mathbf{E}[ (\mathbf{R}^i \mathbf{q}_i)^T \mathbf{R}^j \mathbf{k}_j ] =\mathbf{E}[ (\mathbf{R}^i \mathbf{q}_i)^T ] \mathbb{E}[ \mathbf{R}^j \mathbf{k}_j ] = 0, \\ \text{if } \mathbf{q}_i, \mathbf{k}_j \overset{i.i.d.}{\sim} \mathcal{N}(0; I_d). $$上图右侧变展示这种情况, 并无所预想的那样存在距离衰减的情况 (我自己测试的如下图所示, 即使增大 relative distance 到 100,000 依然没有距离衰减的现象发生.).
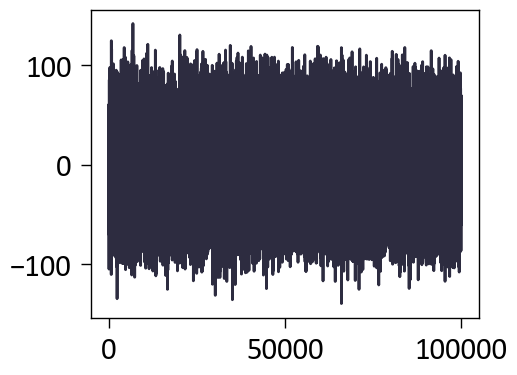
RoPE 的高低频
- 所以 RoPE 究竟为什么会有效呢?
高频
- 首先, 作者直觉上认为, 对于靠前的维度 ($k$ 较小), 其过大的旋转角度会实际上会导致那部分维度所得结果趋于噪声, 因此理论模型不太会直接用到这部分信息:

- 作者给了一个间接的例子: 统计不同层 query 两两维度的模长的平均. 作者假设模长越大, 说明这部分信息越受到模型的重视, 可以发现, 绝大部分能量都集中在低频部分.
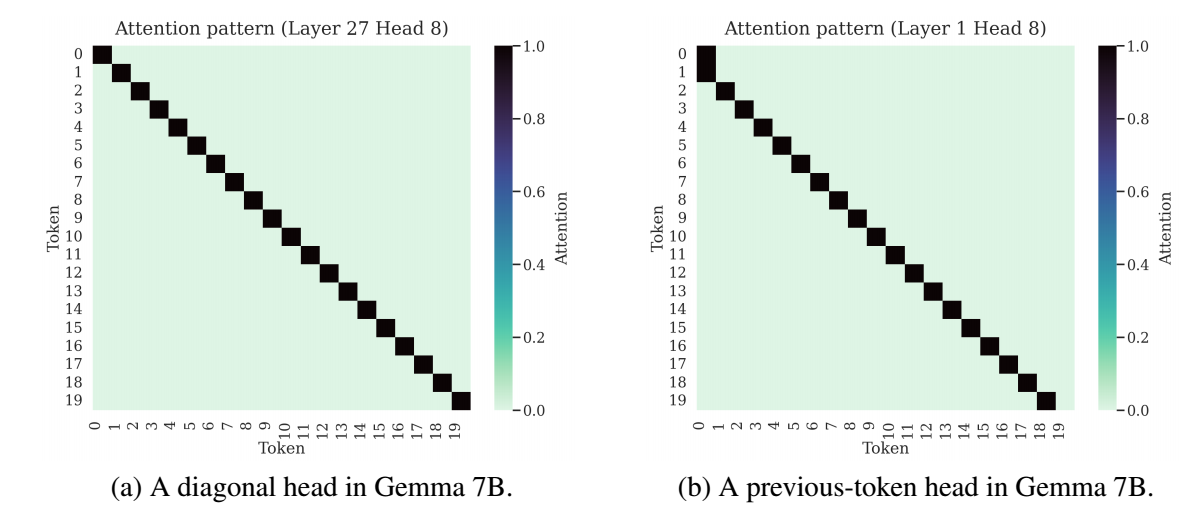
有意思的是, 在最初的一些层和最后一些层, 高频会受到更多的关注. 作者发现, 此时它们的 attnetion 矩阵也非常特殊. 在第一层实际上是一个 ‘previous-token’ 的 attention, 而最后一层则几乎是对角的 attention.
所以作者的猜想是: RoPE 的高频部分实际上为模型生成这些’独特’ attention map 的能力!
作者进一步在理论上证明, 倘若不施加位置编码, 对于重复的序列, 其 attention map 一定不是上述的 ‘diagonal’ 或者 ‘previous-token’ 类型的. 而 RoPE 对于任意的序列, 模型总能通过学习特定模长来实现上述的特殊的 attention map.
总而言之, RoPE 的确赋予了模型一些特殊的能力.
低频
因为维度靠后的角度变化较慢, 所以这些位置实际上决定了模型对于 ‘semantic’ 信息的感知力. 一个经验性的证据是, 为了扩展到更长的上下文, 大家普遍采取增大 $\theta$ 的做法, 这实际上就是减少由于 RoPE 带来的不一致性.
但是, 只要上下文足够长, RoPE 带来的不一致性始终无法完全避免. 为了进一步验证这一点, 其将 RoPE 改进为 $p$-RoPE: 舍弃最低的 $1-p$-fraction 的频率 仅保留其余的 $p$-fraction 的频率.
这相当于 query, key 向量的最靠后的维度是完全不受位置编码的影响, 因而能够完全限度的保留对 ‘semantic’ 的感知力.
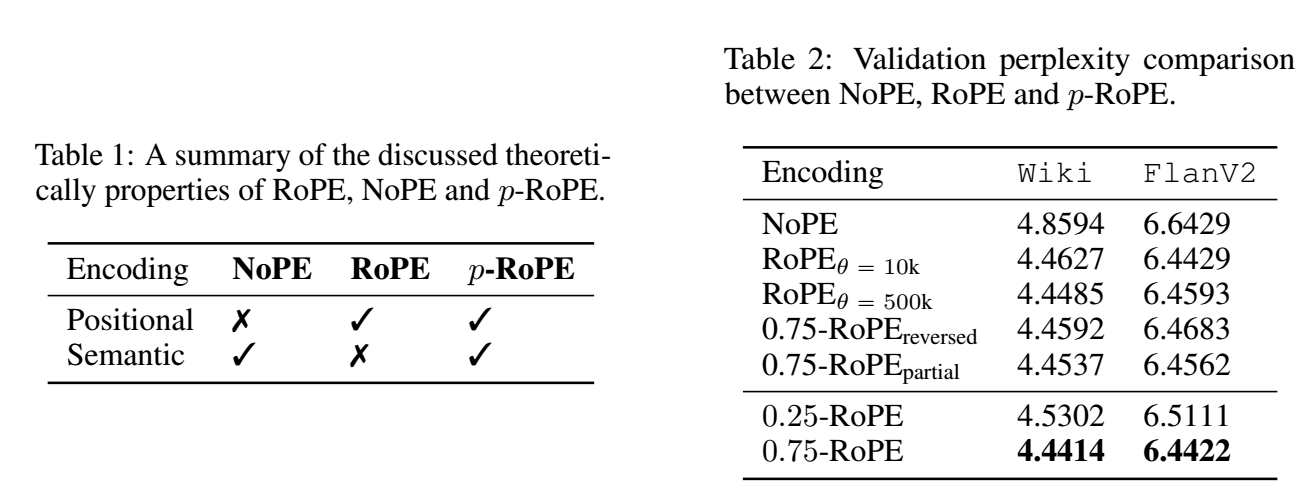
上表展示了 $p$-RoPE 在 $p=0.75$ 的一个优势. 这说明, 的确, RoPE 所引入的位置信息对于最基本的语义信息来说其实本没有多大的必要性.
RoPE 的作者也在他的博客里讨论了部分旋转.