Pareto Multi-Task Learning

预备知识

• (Multi-Objective Learning, MOL) 在现实中, 我们往往有不止一个 (连续可微的) 优化目标 ($T \ll d$)

  $$ \tag{1} f_i: \mathbb{R}^d \rightarrow \mathbb{R}, i=1,2,\ldots, T. $$

  自然, multi-objective learning 就是希望尽可能地让所有的目标都最小. 为了方便起见, 引入向量形式:

  $$ \mathbf{f}: \mathbb{R}^d \rightarrow \mathbb{R}^T, \quad \mathbf{f} = [f_1, f_2, \ldots, f_T]. $$

• (Pareto-Optimal) 显然, 很难有这么理想的情况 $\theta^* \in \mathbb{R}^d$ 恰好是所有目标的 $f_i$ 的最(极)小值点. 因此, 在研究 MOL 的时候, 我们通常追求的是 Pareto-Optimal: $\theta^*$ 是 pareto-optimal 的, 如果不存在 $\theta \in \mathbb{R}^d$ 满足

  $$ \tag{2} \mathbf{f}(\theta) \preceq \mathbf{f}(\theta^*) \text{ and } \exist i, \: f_i(\theta) < f_i(\theta^*). $$

  这里 $\preceq$ 表示 element-wise 的大小比较.

• (Multi-Task Learning, MTL) 一般是通过 linear scalarization, 即通过重加权的方式取得适当的平衡:

  $$ \min_{\theta} \quad \sum_{i=1}^T w_i f_i(\theta), \: w_i \ge 0. $$

  这种方式要求我们细细调节参数, 费时费力.

• (Multiple-Gradient Descent Algorithm, MGDA) 梯度下降几乎是单目标学习的不二法门了, 我们的目标就是探索在多目标的情况下是否依然有这种算法来帮助我们学习. 核心思想是简单的, 令

  $$ \tag{3} \mathbf{g}_i := \nabla_{\theta} f_i \in \mathbb{R}^d, \quad \mathbf{G} := \nabla_{\theta} \mathbf{f} = \left [ \begin{array}{c} \mathbf{g}_1^T \\ \mathbf{g}_2^T \\ \vdots \\ \mathbf{g}_T^T \\ \end{array} \right ] \in \mathbb{R}^{T \times d}. $$

  我们的目标是找到符合所有目标的下降方向 $\mathbf{v}$ 使得

  $$ \tag{4} \mathbf{G}\mathbf{v} = [\mathbf{g}_1^T \mathbf{v}, \mathbf{g}_2^T \mathbf{v}, \ldots, \mathbf{g}_T^T \mathbf{v}] \preceq \mathbf{0}. $$

  如此一来, 通过选择合适的步长 $\eta$, 能够保证

  $$ \mathbf{f}(\theta + \eta \mathbf{v}) \preceq \mathbf{f}(\theta). $$

核心思想

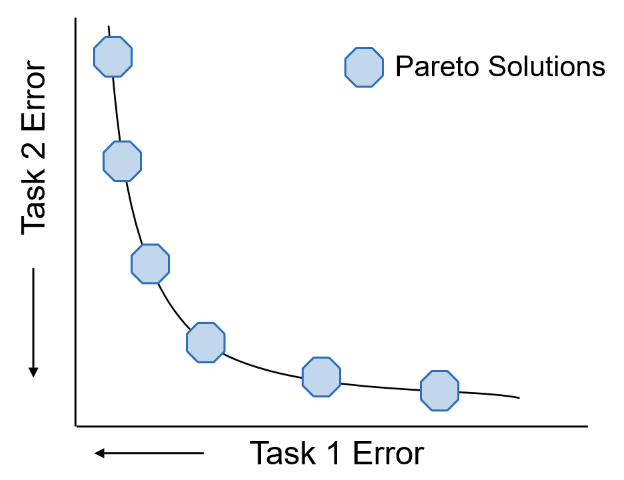
• 本文的研究初衷在 Pareto-optimal 的基础上还要更进一步. 如上图所示, 一整条线上的解都是所谓的 Pareto-optimal 解, 但是在实际中我们总会对最终的结果有一些期望, 比如希望 $f_1 < 1 / 2 f_2$.

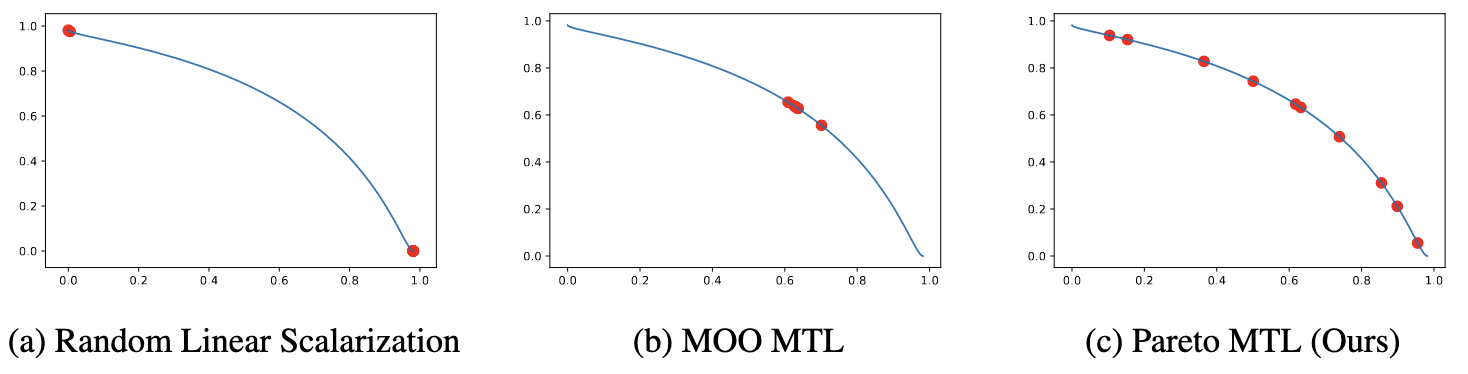
• 如下图所示, 使用 linear scalarization (a) 或者简单的追求 Pareto-optimal (b) 显然是不能反映我们对于’比例’的追求的.

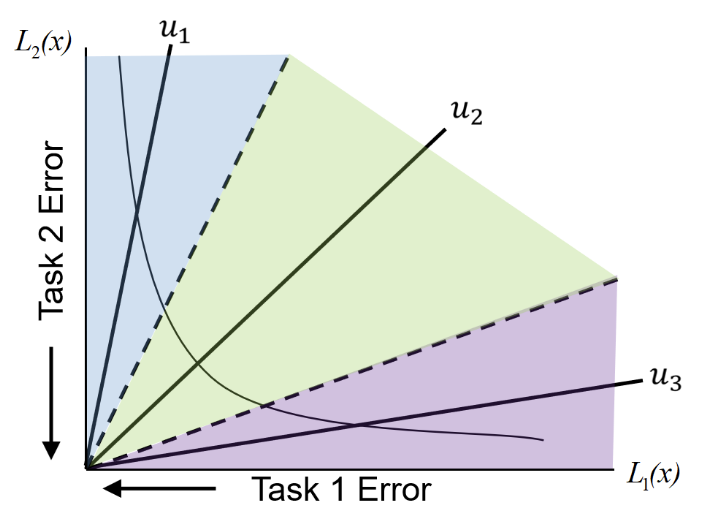
• (Subregions) Pareto MTL 的设计初衷是, 给不同的 Loss 的占比划分不同的区域, 然后在某个区域内进行受限的优化. 如上图所示, 我们可以将整个 loss landscape 切分为由 $\mathbf{u}_1, \mathbf{u}_2, \mathbf{u}_3$ 决定的锥, 倘若假设 $\|\mathbf{u}_1\| = \|\mathbf{u}_2\| = \|\mathbf{u}_3\|$, 则我们有

  $$ \tag{5} \Omega_k = \{ \mathbf{f} \in \mathbb{R}_{+}^2: \mathbf{u}_k^T \mathbf{f} \ge \mathbf{u}_j^T \mathbf{f}, \: j=1,2,3 \}, \quad k=1,2,3. $$

  推广到 $T$ 个目标, $K$ 个区域时为:

  $$ \tag{6} \Omega_k = \{ \mathbf{f} \in \mathbb{R}_{+}^T: \mathbf{u}_k^T \mathbf{f} \ge \mathbf{u}_j^T \mathbf{f}, \: j=1,2, \ldots, K \}, \\ \mathbf{u}_1, \mathbf{u}_2, \ldots, \mathbf{u}_K \in \mathbb{R}_+^T, \: \|\mathbf{u}_1\| =\|\mathbf{u}_2\| =\cdots =\|\mathbf{u}_K\|, \\ k=1,2,\ldots K. $$

• 直观上理解, $\mathbf{u}$ 定义了方向和尺度, 比如 $\mathbf{u} = [0.5, 0.5]$ (未 normalized), 则表明两个目标是同等重要的, $\mathbf{u} = [0.9, 0.1]$ (未 normalized), 则表示 $f_1$ 比起 $f_2$ 更加重要.

• 倘若我们选择了 $\mathbf{u}_k$ 作为尺度, 即希望最终的 loss 分布在 $\mathbf{f} \in \Omega_k$, 即如下的受限优化:

  $$ \tag{7} \begin{align*} \min_{\theta} \quad & \mathbf{f}(\theta) \\ \text{s.t.} \quad & \mathbf{u}_j^T \mathbf{f} \le \mathbf{u}_k^T \mathbf{f}, \quad j=1,2,\ldots, K. \end{align*} $$

• 作者的做法其实很简单, 就是令

  $$ f_{T + j} = (\mathbf{u}_j - \mathbf{u}_k)^T \mathbf{f}, \: j = 1, 2, \ldots, K, $$

• 令 $I_{\epsilon} = \{j: f_{T + j} \ge -\epsilon, \: j=1,2,\ldots, K\}$ 表示那些严重超出区域的情形, 这衍生出一个扩展后的多目标函数:

  $$ \mathbf{\tilde{f}} = \mathbf{f} \| \{f_{T + j}\}_{j \in I_{\epsilon}} \in \mathbb{R}_+^{T + |I_\epsilon|}. $$

• 作者采用 [1] 中的解法, 试图找到一个下降方向 $\mathbf{v} \in \mathbb{R}^d$ 满足

  $$ \tag{8} \begin{align*} \min_{\mathbf{v} \in \mathbb{R}^d, \alpha \in \mathbb{R}} \quad & \alpha + \frac{1}{2} \|\mathbf{v}\|_2^2 \\ \text{s.t.} \quad & \nabla^T f_i(\theta) \mathbf{v} \le \alpha, \: f_i \in \mathbf{\tilde{f}}. \end{align*} $$

• (特别的性质${}^{[1]}$) 如果 $\theta$ 不是 Pareto critical 的 (即至少存在一个 $\mathbf{v} \not = \mathbf{0}$ 满足 $\mathbf{\tilde{f}} (\theta + \eta \mathbf{v}) \prec \mathbf{\tilde{f}}(\theta)$ 对于某个 $\eta > 0$), 则 (8) 的解一定满足

  $$ \tag{9} \nabla^T f_i (\theta) \mathbf{v} \le \alpha < 0, \quad f_i \in \mathbf{\tilde{f}}. $$

  这保证了我们只需要求解 (8) 就可以找到合适的下降方向.

• 定义 $\mathbf{g}_i = \nabla f_i(\theta)$, 引入拉格朗日乘子我们可以得到如下的对偶问题:

  $$ \tag{10} \begin{align*} \max_{\lambda} \: \inf_{\alpha, \mathbf{v}} \quad & \alpha + \frac{1}{2} \|\mathbf{v}\|_2^2 + \sum_i \lambda_i (\mathbf{g}_i^T \mathbf{v} - \alpha) \\ \text{s.t.} \quad & \lambda_i \ge 0, \: \forall i \end{align*} $$

• 根据拉格朗日对偶问题的定义, $\lambda$ 的定义域为使得

  $$ \tag{11} \lambda: \quad g(\lambda) := \inf_{\alpha, \mathbf{v}} \{\alpha + \frac{1}{2} \|\mathbf{v}\|_2^2 + \sum_i \lambda_i (\mathbf{g}_i^T \mathbf{v} - \alpha) \} > -\infty. $$

• 对 (11) 进一步分解, 可以得到

  $$ \tag{12} g(\lambda) = \underbrace{\inf_{\alpha} \left(\sum_{i} \lambda_i - 1 \right) \alpha}_{g_{\alpha}(\lambda)} + \underbrace{\inf_{\mathbf{v}} \left\{ \frac{1}{2} \|\mathbf{v}\|_2^2 + \sum_{i} \lambda_i \mathbf{g}_i^T \mathbf{v} \right\} }_{g_{\mathbf{v}}(\lambda)}. $$

• 因此可得 $g_{\alpha}(\lambda) > -\infty \rightarrow \sum_{i} \lambda_i = 1$, 而

  $$ \tag{13} \frac{1}{2} \|\mathbf{v}\|_2^2 + \sum_{i} \lambda_i \mathbf{g}_i^T \mathbf{v} $$

  仅在 $\mathbf{v} = -\sum_{i}\lambda_i \mathbf{g}_i$ 出取得最小值.

• 因此, 我们可以得到对偶问题的最大值为:

  $$ \tag{14} \begin{align*} \max_{\lambda} \quad & -\frac{1}{2}\| \lambda_i \mathbf{g}_i\|_2^2 \\ \text{s.t.} \quad & \sum_{i} \lambda_i = i, \\ & \lambda_i \ge 0, f_i \in \mathbf{\tilde{f}}. \end{align*} $$

• 问题满足强对偶性, 因此由 (14) 得到的 $\lambda^*$, 以及相应的 $\mathbf{v}^* = -\sum_i \lambda_i^* \mathbf{g}_i$ 就是最优化方向. 而这恰恰也是 MGDA 中所推荐的下降方向, 因此 (14) 也可以用 Frank-wolfe 来求解.

• 当然了, Pareto 和 MGDA 的区别在于, 它自适应地引入一些额外的目标, 这些目标的引入能够帮助最终的解是位于 $\Omega_k$ 的. 而至于哪个区域最合适, 就依赖先验知识或者调参了.

参考文献

1. Fliege J. and Svaiter B. F. Steepest Descent Methods for Multicriteria Optimization. Math Meth Oper Res, 2000. [PDF] [Code]
2. Desideri J. Multiple-Gradient Descent Algorithm (MGDA) for Multiobjective Optimization. C. R. Acad. Sci. Paris, Ser. I, 2012. [PDF] [Code]
3. Sener O. and Koltun V. Multi-Task Learning as Multi-Objective Optimization. NeurIPS, 2018. [PDF] [Code]
4. Lin X., Zhen H., Li Z., Zhang Q. and Kwong S. Pareto Multi-Task Learning. NeurIPS, 2019. [PDF] [Code]