QARM: Quantitative Alignment Multi-Modal Recommendation at Kuaishou
预备知识
- 请了解 RQ-VAE.
核心思想
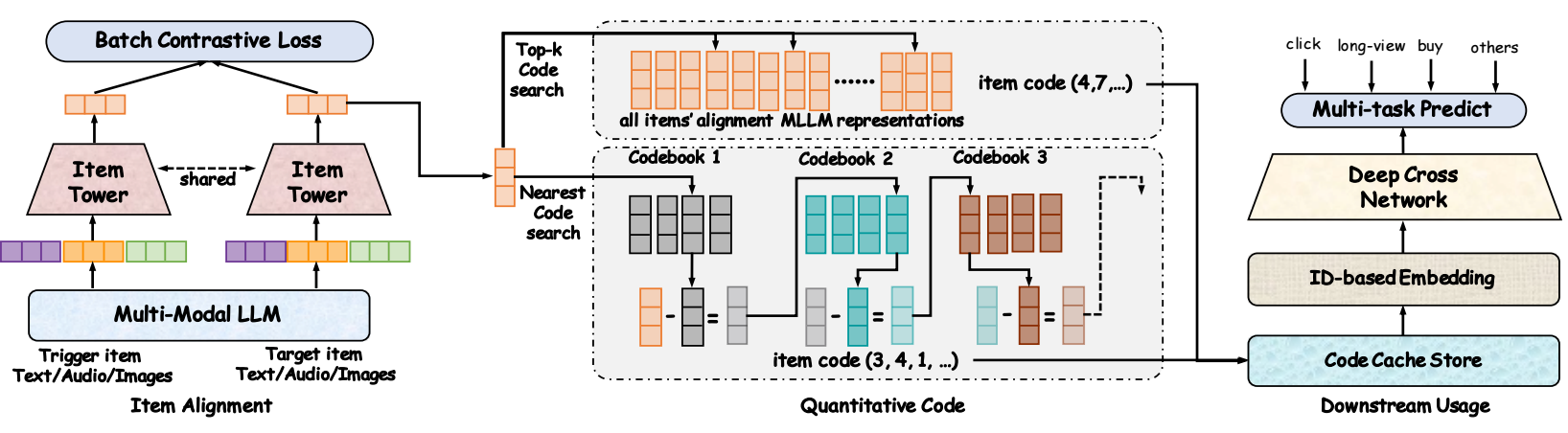
我们知道, 多模态推荐主要涉及:
$$ \text{text/image} \longrightarrow \text{Encoder} \longrightarrow \text{Embedding} \longrightarrow \text{Recommender} $$的过程, 且通常 $\text{Encoder}$ 是通过 CV, NLP 任务预训练好后固定下来的.
作者认为这种方式缺少了推荐任务的约束, 且通常用作 ID embedding 的补充而不是替代. 于是本文就希望:
- 通过推荐任务微调 Encoder;
- 通过向量量化来替代 ID.
Item Alignment of QARM
QARM 首先通过 Item-Item 的匹配任务来约束 Encoder, 即 Item 和它在推荐上’相似’的 Item 靠近, ‘不相似’的远离. 这里的相似 Item 通过如下的两种方式得到:
- 通过过往的 User2Item 检索模型: 为每个用户所 positive clicked target item 选择最相似的 Item;
- 通过过往的 Item2Item 检索模型: 为每个 item 选择高相似度的 Item.
得到高相似度的 Item pairs 之后, 通过对比学习进行训练:
$$ \textbf{M}_{\text{trigger}} = \text{MLLM}( \mathbf{T}_{\text{trigger}}^{\text{text}}, \mathbf{T}_{\text{trigger}}^{\text{audio}}, \mathbf{T}_{\text{trigger}}^{\text{image}} ), \\ \textbf{M}_{\text{target}} = \text{MLLM}( \mathbf{T}_{\text{target}}^{\text{text}}, \mathbf{T}_{\text{target}}^{\text{audio}}, \mathbf{T}_{\text{target}}^{\text{image}} ), \\ \mathcal{L}_{\text{align}} = \text{Batch-Contrastive}( \mathbf{M}_{\text{trigger}}, \mathbf{M}_{\text{target}}, \mathcal{B} ). $$这里 $\text{MLLM}$ 是需要微调的 Encoder.
Quantitative Code of QARM
QARM 不采取之前常用的 RQ-VAE.
作者认为既然先前已经对 Encoder 进行微调了, 我们只需要从得到的 embeddings 中估计一些聚类中心, 即可作为 codebook. 当然了, 如果我们还希望使用 RQ-VAE 的格式, 就需要为每一层筛选 codebook $\mathbf{R}^l \in \mathbb{R}^{K \times d}, \: l=1,2,\ldots, L$:
将所有 item 喂入 Encoder 得到 embedding table $\mathbf{M}^{(0)} \in \mathbb{R}^{N \times d}$.
通过 Kmeans 得到 $K$ 个聚类中心, 作为 $\mathbf{R}^1$.
为 $\mathbf{M}^{(0)}$ 中的每个 embedding 通过最近邻匹配上述的聚类中心, 得到 $\mathbf{\hat{M}}^{(0)}$.
得到下一步的 embedding table $\mathbf{M}^{(1)} = \mathbf{M}^{(0)} - \mathbf{\hat{M}}^{(0)}$.
重复上述过程, 得到
$$ \mathbf{R}^1, \mathbf{R}^2, \ldots, \mathbf{R}^L. $$
接下来, 对于一个 embedding $\mathbf{m} \in \mathbf{M}^{(0)}$, 我们可以通过如下方式得到它的离散编码 $(r_1, r_2, \ldots, r_L)$:
$$ r_1 = \text{NearestCode}(\mathbf{R}^1, m, 1), \quad \mathbf{m}^1 = \mathbf{m} - \mathbf{R}_{r_1}^1, \\ r_2 = \text{NearestCode}(\mathbf{R}^2, m^1, 1), \quad \mathbf{m}^2 = \mathbf{m}^1 - \mathbf{R}_{r_2}^2, \\ \cdots, r_{L} = \text{NearestCode}(\mathbf{R}^L, \mathbf{m}^{L-1}, 1). $$此即可用于后续的训练.