R2MR: Review and Rewrite Modality for Recommendation
预备知识
- (Multimodal Collaborative Filtering) 多模态协同过滤, 一般是综合 Textual, Visual, ID 特征得到 Item 的表征. 然后通过某种方式计算 User/Item 间的得分用于预测. 多模态协同过滤的很重要的一个课题便是如何去除模态中的无关信息.
核心思想
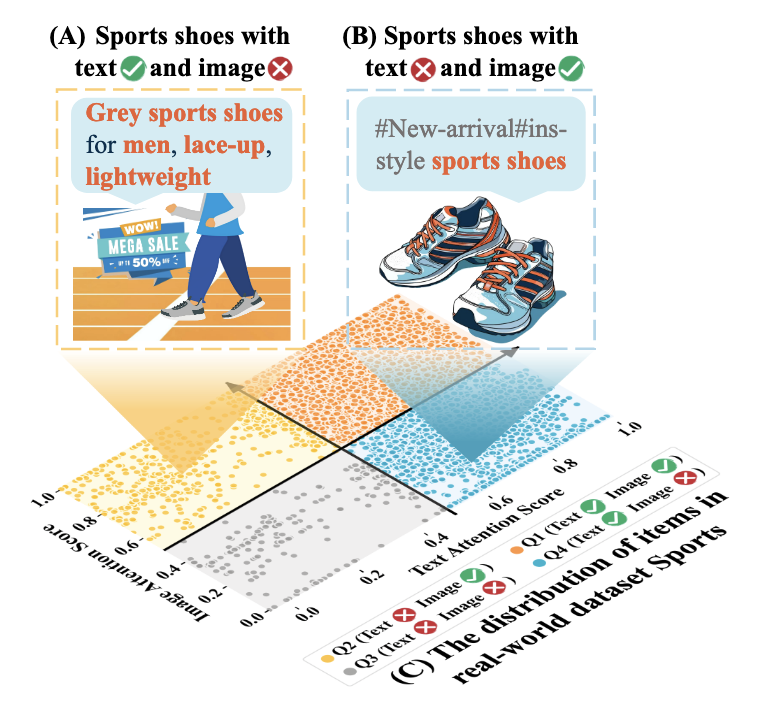
R2MR 认为简单地将不同的模态特征融合起来会有很大的问题, 因为同一个 Item 的 Textual/Visual 的特征的质量可能是有很大差异的. 如上图所示, 都是 Sports shoes, (A) 的文本描述非常详实但是图片中鞋子并不是主题, 因此具有高质量的 Textual 特征但是低质量的 Visual 特征; 与之相反的, (B) 代表了具有高质量 Visual 特征但是低质量 Textual 特征的情况.
(Motivation) R2MR 希望定位模态特征的质量, 并训练一个模型将低质量的特征转换为高质量特征, 最后用于多模态推荐.
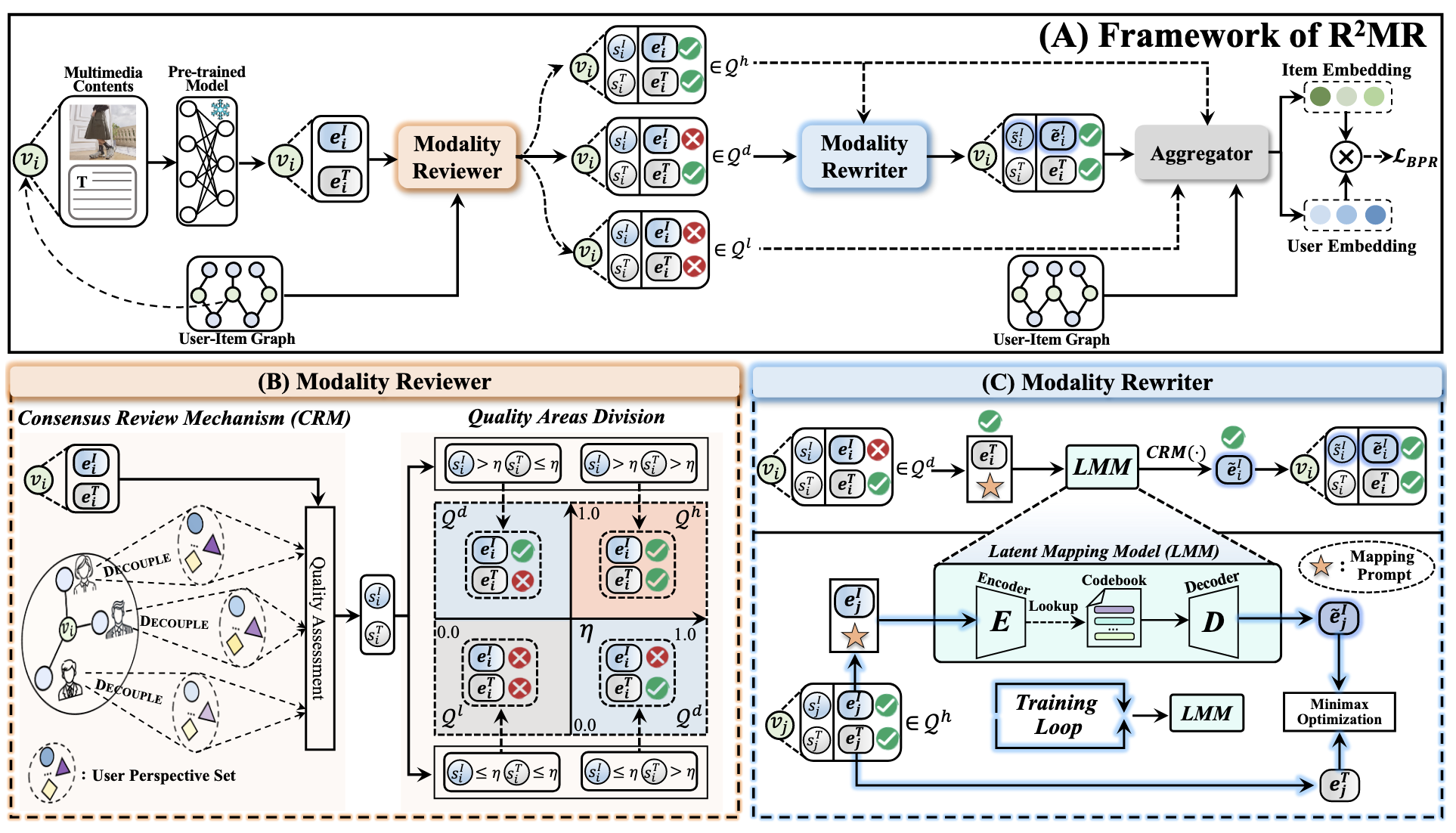
(Modality Reviewer: 定位模态特征质量) 首先, 我们需要通过某种方式来定位特征质量.
对于 User $u_i$ 赋予 Embedding $\mathbf{u}_i \in \mathbb{R}^d$;
分解为 $K$ 个不同的表示:
$$ \mathcal{P}_i = \{ \mathbf{p}_i^1, \mathbf{p}_i^2, \ldots, \mathbf{p}_i^K \} = \text{DECOUPLE}(\mathbf{u}_i) = \mathcal{R}(\mathbf{u}_i \cdot \mathbf{W}_u), $$其中 $\mathbf{W}_u \in \mathbb{R}^{d \times Kd}$, $\mathcal{R}$ 表示 reshape 操作.
令 $\mathcal{N}_i$ 表示所有与 item $i$ 存在交互的 user 的集合, 则 item $i$ 的 模态 $m$ 的 score 定义为:
$$ s_i := \text{Mean} \left( \{\sigma(\mathbf{\tilde{e}}_i^m \cdot \mathbf{p}_j^k): j \in \mathcal{N}_i, k=1,2,\ldots, K\} \right), $$这里 $\mathbf{\tilde{e}}_i^m = \mathbf{e}_i^m \cdot \mathbf{W}$, $\mathbf{e}_i^m, m \in \{T, I\}$ 表示模态特征 (作者预先通过 PCA 预处理保证不同模态维度是一致的).
定义模态特征的三种状态:
$$ \begin{align*} (\text{high-quality}) \quad & s_i^T > \eta \wedge s_i^I > \eta, \\ (\text{disparity}) \quad & s_i^T > \eta \oplus s_i^T > \eta, \\ (\text{low-quality}) \quad & s_i^T < \eta \wedge s_i^I < \eta. \\ \end{align*} $$这里 $\oplus$ 表示恰好有一个条件满足. 即 (disparity) 表示 Textual/Visual 特征有一个是高质量的另一个是低质量的.
(Modality Rewriter: 生成高质量模态特征) R2MR 训练一个 VQGAN 通过其中一个高质量模态预测另一个潜在的高质量模态:
首先在 high-quality 的基础上进行训练, 特别地, 模型的输入为
$$ \mathbf{\tilde{e}}_i^{tgt} = LMM(\mathbf{e}_i^{src}, \mathbf{p}^{s \rightarrow t}; \theta^{LMM}), $$这里 $\mathbf{p}^{s\rightarrow t} \in \{\mathbf{p}^{T \rightarrow I}, \mathbf{p}^{V \rightarrow T} \}$ 类似与 Mask Token.
生成 disparity 的 item 的高质量模态特征 $\mathbf{\tilde{e}}_i^m$: 是否保留取决于 Modality Reviewer 给与它的分数是否高于原本 $\mathbf{e}_i^m$ 的.
(Recommendation Model) 在上面的基础上, 我们可以得到 Item 的一个融合表示:
$$ \mathbf{\tilde{h}}_i = \|_{m \in \{T, I\}} (\bar{s}_i^m \mathbf{\bar{e}}_i^m + (1 - \bar{s}_i^m) \mathbf{h}_i). $$这里 $\|$ 表示向量拼接操作. $\mathbf{h}_i$ 是 Item ID embedding. $\bar{s}, \bar{\mathbf{e}}$ 取决于模态用的是原本的模态特征还是改进后的模态特征. 后续的操作就和普通的多模态协同过滤差不多了.
注: 本文细节有点多, 我不得不省略一些内容, 希望我已经把重点讲明白了.