RankMixer: Scaling Up Ranking Models in Industrial Recommenders
预备知识
- (Recommendation Foundation Model) 当下很多公司都致力于将推荐模型扩大的研究, 其最大好处能够大大提高计算资源的利用率. 和 Tiger 以及 OneRec 不同, 抖音依旧在探索 CTR 模型的上限.
核心思想
(设计原则)
- 推荐是一个很吃延迟的任务, 因此, 设计的模型应当具有相当的计算效率, 传统的 Transformer 架构在一点上并不那么优秀.
- 和 NLP 任务不同, 推荐的 token embedding 往往来自不同的特征空间, 因此类似 self-attention 等融合机制并不合适.
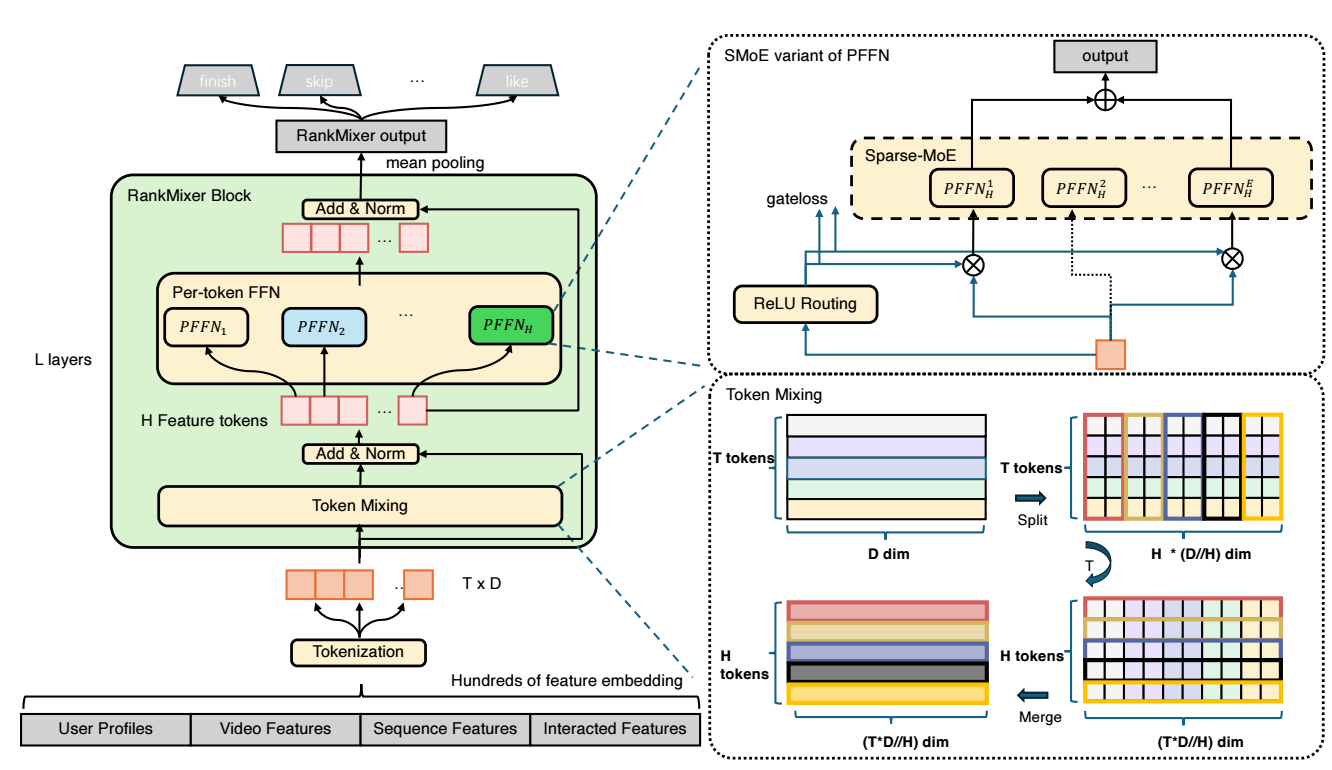
(整体架构) 整体架构其实很简单:
首先通过某种方式得到信息密度较高的 feature tokens $\mathbf{x}_1, \mathbf{x}_2, \ldots, \mathbf{x}_T$;
RankMixer 的每个 block 按照如下方式进行:
$$ \mathbf{S}_{n-1} = \text{LN}(\text{TokenMixing}(\mathbf{X}_{n-1}) + \mathbf{X}_{n-1}), \\ \mathbf{X}_n = \text{LN}(\text{PFFN}(\mathbf{S}_{n-1}) + \mathbf{S}_{n-1}). $$其中 $\text{LN}(\cdot)$ 表示 LayerNorm, $\mathbf{X}_n \in \mathbb{R}^{T \times D}$ 为每一层的输出.
最后输出为 $\mathbf{X}_L \in \mathbb{R}^{T \times D}$, 对 $T$ 轴进行 mean pooling 用于下游任务 (e.g., CTR).
(Feature Tokenization) 和传统的 CTR 模型一样, 输入特征以 user profiles, video features, … 等为基础. 但是, 如果一一嵌入会导致一个很大的 $T$, 导致后续计算的大大增加, 为了弥补, 就需要降低 embedding size $D$ 了. 鉴于特征之间存在较大的冗余, RankMixer 首先将特征进行聚类分组, 最后保留 $N$ 个类:
$$ \mathbf{e}_{\text{input}} = [\mathbf{e}_1 \| \mathbf{e}_2 \| \ldots \| \mathbf{e}_N]. $$接着, token embeddings 通过如下方式得到:
$$ \mathbf{x}_i = \text{Proj}(\mathbf{e}_{\text{input}} [d \cdot (i - 1): d \cdot i] ), i = 1,\ldots, T. $$(TokenMixing) CTR 模型最重要的就是特征交叉了, TokenMixing 就是负责这个.
首先将每个 token embedding 分解为多个 heads:
$$ [\mathbf{x}_t^{(1)} \| \mathbf{x}_t^{(2)} \| \ldots \| \mathbf{x}_t^{H}] = \text{SplitHead}(\mathbf{x}_t). $$将每个 head 的 $T$ tokens 拼接起来
$$ \mathbf{s}^{(h)} = [\mathbf{x}_1^{(h)} \| \mathbf{x}_2^{(h)} \| \ldots \| \mathbf{x}_T^{(h)}] \in \mathbb{R}^{TD / H}. $$为了保证 residual connection 的可行性, RankMixer 强制要求 $H = T$, 最终的输出为:
$$ \mathbf{s}_1, \mathbf{s}_2, \ldots, \mathbf{s}_T = \text{LN}( \text{TokenMixing}(\mathbf{x}_1, \mathbf{x}_2, \ldots, \mathbf{x}_T) + (\mathbf{x}_1, \mathbf{x}_2, \ldots, \mathbf{x}_T) ). $$
(PFFN, Per-token FFN) 和传统的 Transformer 的 FFN 不同, RankMixer 对于每一个 token 设置一个独立的 FFN (可行的原因是 RankMixer 是序列长度固定的):
对于每一个 token embedding $\mathbf{s}_t$, 进行如下操作
$$ \mathbf{v}_t = f_{\text{pffn}}^{t, 2}( \text{GELU}( f_{\text{pffn}}^{t, 1} (\mathbf{s}_t) ) ), \\ f_{\text{pffn}}^{t, i}(\mathbf{x}) = \mathbf{x} \mathbf{W}_{\text{pffn}}^{t, i} + \mathbf{b}_{\text{pffn}}^{t, i}, \quad t=1,2,\ldots, T. $$
(Sparse MoE) 特别地, 为了进一步高效地增加参数量, RankMixer 中每一个 Dense PFFN 用 Sparse Mixture-of-Experts (MoE) 替代. 通过 ReLU 而非 Softmax + Top-K 激活 Experts, 并且通过自适应的 $\ell_1$ 惩罚加以约束.