Think Before Recommend: Unleashing the Latent Reasoning Power for Sequential Recommendation
预备知识
- $\mathcal{U}$, user set, $|\mathcal{U}| = M$;
- $\mathcal{V}$, item set, $|\mathcal{V}| = N$;
- $\mathcal{S}^u = [v_1^u, v_2^u, \ldots, v_{n_u}^u]$, 用户 $u$ 的交互序列.
核心思想
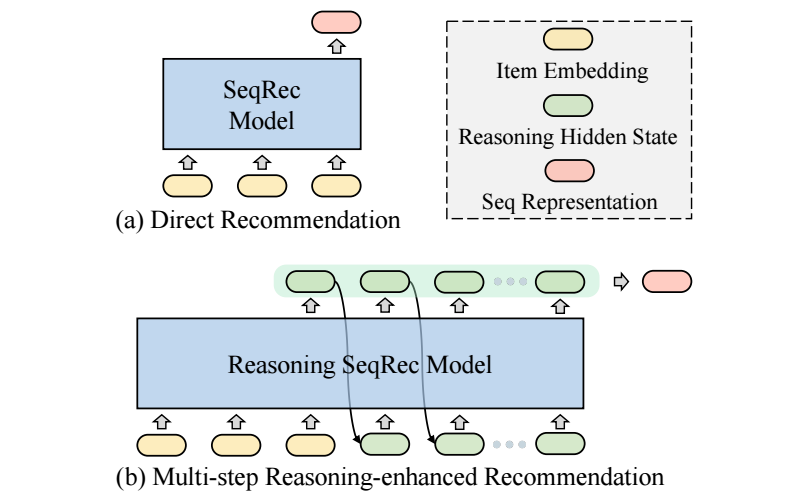
一般的序列推荐模型 (e.g., SASRec), 对应位置的输入 embedding 用于预测 next-item (如上图 (a) 所示).
在 LLM 领域, CoT (chain-of-thought) 已经被证明在各领域上性能提高的优势了. 实际上, CoT 实际上是促使模型进行多次推理以获得更为准确可靠的结果. 那么类似的思想能不能推广到推荐呢? 这衍生了本文的 ReaRec.
假设第 $i$ 个位置的输入是 $\mathbf{h}_i^0$, 故整个序列的输入为:
$$ \mathbf{H}^{0} = [\mathbf{h}_1^0, \mathbf{h}_2^0, \ldots, \mathbf{h}_n^0] \in \mathbb{R}^{n \times d}. $$经过 $L$ 个 transformer blocks 之后, 我们可以得到输出特征:
$$ \mathbf{H}^{L} = [\mathbf{h}_1^L, \mathbf{h}_2^L, \ldots, \mathbf{h}_n^L]. $$接下来, 令 $\mathbf{h}_{n+1}^0 = \mathbf{h}_n^L + \mathbf{p}_{n+1}^R$, 这里 $\mathbf{p}_{n+1}^R$ 是特别的 reasoning position embedding.
如此以往, 我们可以得到
$$ \mathbf{H}^{L} = [\mathbf{h}_1^L, \mathbf{h}_2^L, \ldots, \mathbf{h}_n^L, \underbrace{\mathbf{h}_{n+1}^L, \ldots, \mathbf{h}_{n+k}^L}_{=: \mathbf{R} \in \mathbb{R}^{k \times d}}]. $$为了符号简便, 重新记 $\mathbf{r}_i = \mathbf{h}_{n+i}$.
接下来就是这么利用 $\mathbf{R}$ 以及如何训练使得其有意义.
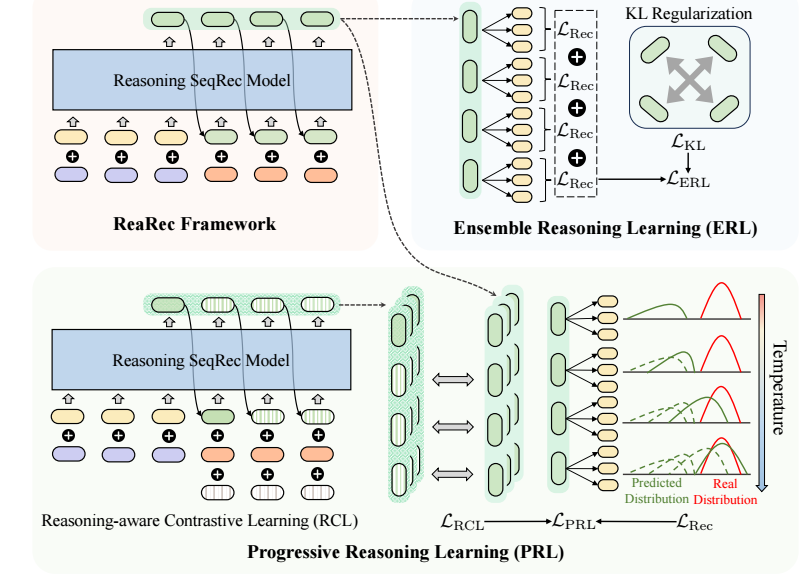
Ensemble Reasoning Learning (ERL)
ERL 将 $k$ 的平均作为 user 的表示:
$$ \mathbf{h}_u = \frac{1}{k} \sum_{i=1}^k \mathbf{r}_i^{L}. $$然后通过内积可以用于预测.
训练稍有不同, 不是直接拿 $\mathbf{h}_u$ 进行训练, 它要求每个阶段的表示 $\mathbf{r}_i^L$ 都和 target 匹配:
$$ \mathcal{L}_{\text{Rec}} = -\sum_{i=1}^k \log \hat{y}_{v_+}^{i}, \\ \hat{y}_{v_+}^i = [\text{softmax}( \mathbf{r}_k \cdot \mathbf{E}^T)]_{v^+}, $$这里 $\mathbf{E}$ 是所有 item 的初始 embeddings.
同时要求不同的阶段尽可能表示不同含义, 以满足多样性 (就像 ensemble learning 里面通常也要求不同的模型具有不同的特点):
$$ \mathcal{L}_{\text{KL}} = -\sum_{i=1}^k \sum_{j=i+1}^k \text{KL}( \hat{y}^i \| \hat{y}^j ). $$最小化 $\mathcal{L}_{\text{KL}}$ 等价于最大化两两的 KL 散度, 以获取多样性 (原文应该漏了一个 ‘-’).
ERL 的损失即为
$$ \mathcal{L}_{\text{ERL}} = \mathcal{L}_{\text{Rec}} + \lambda \mathcal{L}_{\text{KL}}. $$
Progressive Reasoning Learning (PRL)
PRL 用最后一个 $\mathbf{h}_u = \mathbf{r}_k^L$ 作为用户的表示.
PRL 是希望在一步一步推理过程中, 模型对自己的预测变得越发自信, 所以首先 在原本的 $\mathcal{L}_{\text{Rec}}$ 中引入一个 Progressive Temperature Annealing:
$$ \hat{y}^i = \text{softmax}(\mathbf{r}_i^L \cdot \mathbf{E}^T / \tau_i), \\ \tau_i = \tau \cdot \alpha^{k - i}. $$即越往后训练难度越大, 这就要求模型越往后变得越发自信.
除此之外, 作者额外引入一个对比学习损失来增强模型的鲁棒性:
$$ \mathcal{L}_{\text{RCL}} = -\sum_{i=1}^k \log \frac{ \exp(\text{sim}(\mathbf{\tilde{r}}_i^L, \mathbf{r}_i^+ / \tau)) }{ \exp(\text{sim}(\mathbf{\tilde{r}}_i^L, \mathbf{r}_i^+ / \tau)) + \sum_{\mathbf{r}_i^- \in \mathbf{R}_i^-}\exp(\text{sim}(\mathbf{\tilde{r}}_i^L, \mathbf{r}_i^- / \tau)) }, $$其中 $\mathbf{\tilde{r}}$ 以 $\mathbf{\tilde{r}}_i^0 = \mathbf{r}_i + \bm{\epsilon}$ 为输入得到的特征 ($\bm{\epsilon}$ 采样自一个正态分布 $\mathcal{N}(\bm{0}, \gamma \bm{I})$). $\mathbf{r}_i^+, \mathbf{r}_i^-$ 则分别表示正负样本.
于是训练损失为
$$ \mathcal{L}_{\mathbf{PRL}} = \mathcal{L}_{\text{Rec}} + \mathcal{L}_{\text{RCL}}. $$