Autoregressive Image Generation using Residual Quantization
预备知识
- 请务必了解 VQ-VAE.
核心思想
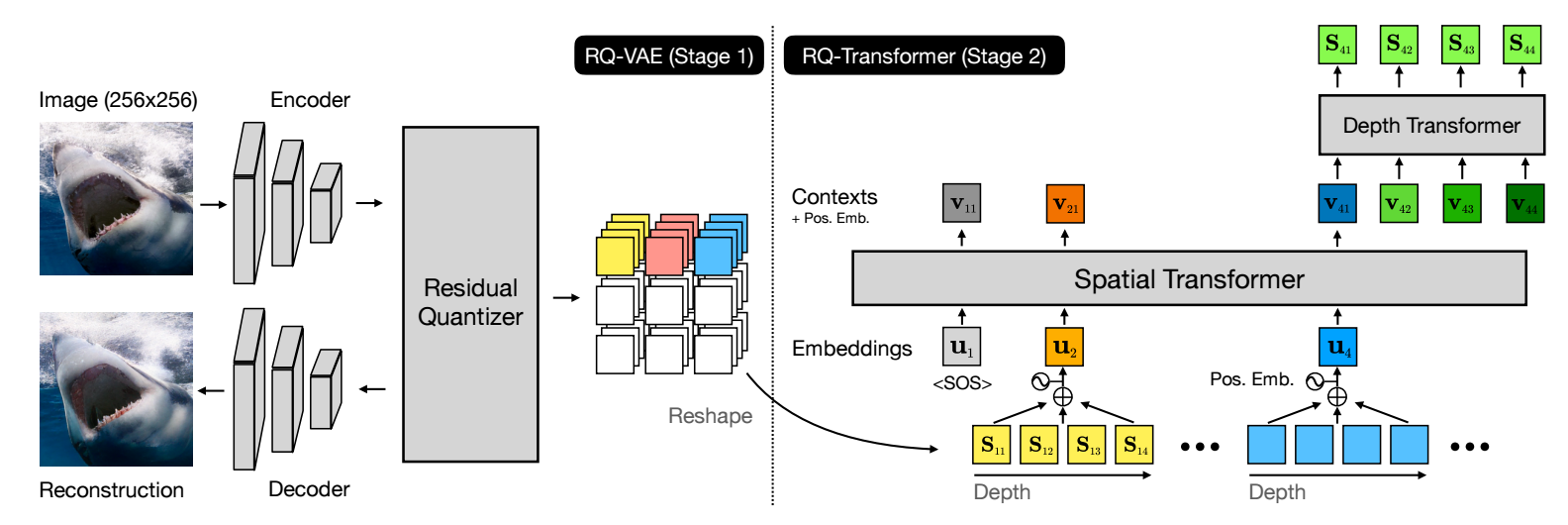
RQ-VAE 自称也是为了解决所谓的 codebook collapse 问题, 即当 codebook size 逐渐增加的时候, 或有越来越多的向量变得"冗余".
另一方面, 如果我们减少 codebook size, 很容易相当在向量量化的过程会造成非常大的信息损耗. 于是, 本文提出了 RQ-VAE, 本质上是一个向量逐步地匹配 $D$ 个向量, 而非 one-to-one 的模式.
RQ-VAE 的过程可以如此形式化:
给定图片输入 $\mathbf{X} \in \mathbb{R}^{H_o \times W_o \times 3}$;
经过 Encoder $E$ 得到
$$ \mathbf{Z} = E(\mathbf{X}) \in \mathbb{R}^{ \underbrace{H_o / f}_{=: H} \times \underbrace{W_o / f}_{=: W} \times n_z }; $$给定 codebook $\mathcal{C} = \{\mathbf{e}_k\}_{k \in [K]}$, 进行向量量化:
$$ Q(\mathbf{z} \in \mathbb{R}^{n_z}; \mathcal{C}) = \text{argmin}_{k \in [K]} \|\mathbf{z} - \mathbf{e}_k \|_2^2, $$对于 $\mathbf{Z}$ 来说, 可以得到如下的 codes:
$$ \mathbf{M}^{(1)} \in [K]^{H \times W}, \\ \mathbf{M}_{hw}^{(1)} = Q(\mathbf{Z}_{hw}; \mathcal{C}); $$计算量化之后的残差
$$ \mathbf{R}^{(d)} = \mathbf{R}^{(d-1)} - \mathbf{E}_{\mathbf{M}^{(d)}}, \quad d \ge 1, \\ \mathbf{R}^{(0)} = \mathbf{Z}. $$这里 $\mathbf{E}_{\mathbf{M}^{(0)}} \in \mathbb{R}^{H \times W \times n_z}$ 表示对应 codes 的向量表示. 将 $\mathbf{R}^{(d)}$ 重新上述的向量量化过程.
假设我们总归进行了 $D$ 步残差量化, 我们可以得到
$$ \mathbf{M} \in \mathbb{R}^{H \times W \times D} $$的 codes.
通过 Decoder $G$ 恢复图像:
$$ \mathbf{\hat{X}} = G(\mathbf{\hat{Z}}), \quad \mathbf{\hat{Z}} = \sum_{d=1}^D \mathbf{E}_{\mathbf{M}^{(d)}}. $$
容易发现, 残差量化实际上就是希望一步一步地用 codebook 来表示自己 (有点 PCA 降维的感觉). 所以它的训练目标也是类似的:
$$ \mathcal{L}_{\text{recon}} = \|\mathbf{X} - \mathbf{\hat{X}} \|_2^2, \\ \mathcal{L}_{\text{commit}} = \sum_{d=1}^D \bigg \| \mathbf{Z} - \text{sg} \big[ \mathbf{\hat{Z}}^{(d)} \big] \bigg \|_2^2, \\ \mathbf{\hat{Z}}^{(d)} = \sum_{d'=1}^d \mathbf{E}_{\mathbf{M}^{(d')}}. $$注意到, 这里的 commit loss 部分, 要求 $\mathbf{Z}$ 和每一个累积的近似部分近似, 以鼓励每个量化阶段都能抓住足够的信息, 此外这里吧 VQ-VAE 中的 $\|\text{sg}(\mathbf{Z}) - \mathbf{\hat{Z}}\|$ 给删掉了, 这部分主要用于 codebook 的监督和更新. 这里作者说:
The codebook $\mathcal{C}$ is updated by the exponential moving average.
此外, RQ-VAE 也用了 VQGAN 里建议的 adversarial training 用来提高生成图片的质量.
通过上面的部分我们就能够进行有效的量化了, 至于怎么使用中间的离散表示就仁者见仁智者见智了. 本文给的建议是 (如上图所示) 按照 depth 相加得到一个个 token (相当于就是用 $\mathbf{\hat{Z}}$ 预测后续的 token).