A Self-Attentive Model for Knowledge Tracing
预备知识
请先了解 DKT.
$e \in [E] = \{0, 1, 2, \ldots, E - 1\}$, 习题的序号;
$r \in \{0, 1\}$, 习题 $e$ 某个学生做对与否.
核心思想
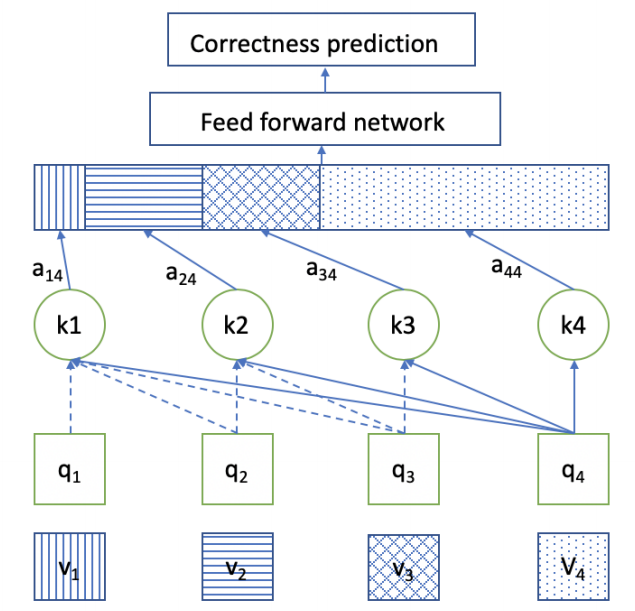
本文几乎就是 GPT (decoder-only) 的 transformer 在 DKT 上的应用: SAKT 希望根据学生的交互序列 $\{(e_1, r_1), \ldots, (e_t, r_t)\}$ 预测下一题 $e_{t+1}$ 的做对做错的情况.
由上述描述可知, 与一般的 Transformer 稍有不同, SAKT 在推理过程中需要同时 “见到” 交互序列 以及需要被预测的新的题目.
对于学生的交互序列 $\{(e_1, r_1), \ldots, (e_t, r_t)\}$, 首先得到输入的 token:
$$ y_i = e_i + r_i \cdot E = \left \{ \begin{array}{ll} e_i, & \text{if } r_i = 0, \\ e_i + E, & \text{otherwise}. \end{array} \right . $$即, 对于每个题, 我们需要训练两个独立的 token 以分别对应做对做错. 然后通过 embedding table $\mathbf{M} \in \mathbb{R}^{2E \times d}$ 得到交互序列的向量表示:
$$ \mathbf{\hat{M}} \in \mathbb{R}^{n \times d}. $$这里 $n$ 是序列长度, 短补零长截断.
对于学生的做题序列 $\{e_2, \ldots, e_{t+1}\}$, 通过 embedding table $\mathbf{E} \in \mathbb{R}^{E \times d}$ 得到
$$ \mathbf{\hat{E}} \in \mathbb{R}^{n \times d}. $$两个序列同时喂入 Transformer, 前者用于生成 Key, Value, 后者用于生成 Query:
$$ \mathbf{Q} = \mathbf{\hat{E}} \mathbf{W}^Q, \mathbf{K} = \mathbf{\hat{M}} \mathbf{W}^K, \mathbf{V} = \mathbf{\hat{M}} \mathbf{W}^V, $$其余的和传统的 causal transformer 类似. 注意到, 因为 causal attention 的缘故, 我们能够保证, 在预测 $e_{t+1}$ 的对错时仅依赖 $e_{< t+1}, r_{< t + 1}$ 的信息.
通过 transformer 得到的第 $i$-th 位置的特征 $\bm{f}_i$ 用于预测 $i+1$ 位置:
$$ p_i = \text{Sigmoid}(\mathbf{F}_i \mathbf{w} + \mathbf{b}). $$并通过 BCE 进行训练.