On the Reliability of Sampling Strategies in Offline Recommender Evaluation

预备知识

• (Ranking) 在推荐中, 常见的有两种评价方式:

  1. Full ranking: 即用户选择的正样本和所有的负样本放在一起排序.
  2. Sampled-based ranking: 由于在推荐中 Item 的数量过多, 全部采取 full ranking 的代价太高, 因此有些时候会用 “1 vs n” 的方式, 这里 $n$ 是通过某种方式采样得到的负样本.

• 有趣的是, 在 2020 年 KDD best paper [1] 中, 证明 $n$ 的数量如果不够的话, Sampled-based ranking 会导致不同的 metrics (e.g., Recall, NDCG) 都退化为 AUC.

• (Exposure Bias) 其实在评价领域还有一个非常严重的问题: 曝光偏差. 一方面, 它使得训练本身有偏, 另一方面, 评估的时候, 我们采样的负样本可能实际上是正样本, 因此即使是采取 Full Ranking 也不一定就真实反映一个模型的优劣.

核心思想

数据的设定

• 首先, 我们可以假设有这样一个 Ground Truth 的全知的矩阵 $G \in \mathbb{R}^{|\mathcal{U}| \times |\mathcal{V}|}$ 存在, 这里 $|\mathcal{U}|, |\mathcal{V}|$ 分别表示 user, item 的数量. 举一个如下的简单例子 (简单起见, 1 表示喜欢, 0 表示不喜欢):

  $$ \begin{align} G = \left [ \begin{array}{ccccc} 0 & 1 & 1 & 1 & 0 \\ 1 & 0 & 1 & 0 & 0 \\ 1 & 1 & 1 & 1 & 1 \\ 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \\ \end{array} \right ]. \end{align} $$

• 由于 Exposure Bias/有限观测力 的存在, 我们实际只能观测到如下的矩阵 (? 表示没有观测到):

  $$ \begin{align} L = \left [ \begin{array}{ccccc} ? & ? & 1 & 1 & 0 \\ ? & 0 & 1 & 0 & ? \\ 1 & ? & ? & ? & 1 \\ 0 & ? & 1 & ? & ? \\ ? & 0 & ? & 0 & ? \\ \end{array} \right ]. \end{align} $$

• 当我们想要通过 sampled-based ranking 方法进行评估的时候, 我们会得到一个采样后的矩阵 (-1 表示我们采样的’负样本’):

  $$ \begin{align} L_S = \left [ \begin{array}{ccccc} -1 & -1 & 1 & 1 & 0 \\ -1 & 0 & 1 & 0 & -1 \\ 1 & ? & -1 & -1 & 1 \\ 0 & -1 & 1 & -1 & ? \\ ? & 0 & -1 & 0 & -1 \\ \end{array} \right ]. \end{align} $$

• 每个 $L_S$ 都有一个对应 Ground Truth $G_S$:

  $$ \begin{align} G_S = \left [ \begin{array}{ccccc} 0 & 1 & 1 & 1 & 0 \\ 1 & 0 & 1 & 0 & 0 \\ 1 & ? & 1 & 1 & 1 \\ 0 & 0 & 1 & 0 & ? \\ ? & 0 & 0 & 0 & 0 \\ \end{array} \right ]. \end{align} $$

• 我们只能做到在 $L_S$ 评估, 它得到结果与在 $G_S, G$ 上直接评估存在一定差距, 本文所关心的点就是这个差距是否会导致对不同模型的评价失衡, 以及是否有什么采样方法能够对这种 bias 有一定的免疫力.

数据的模拟

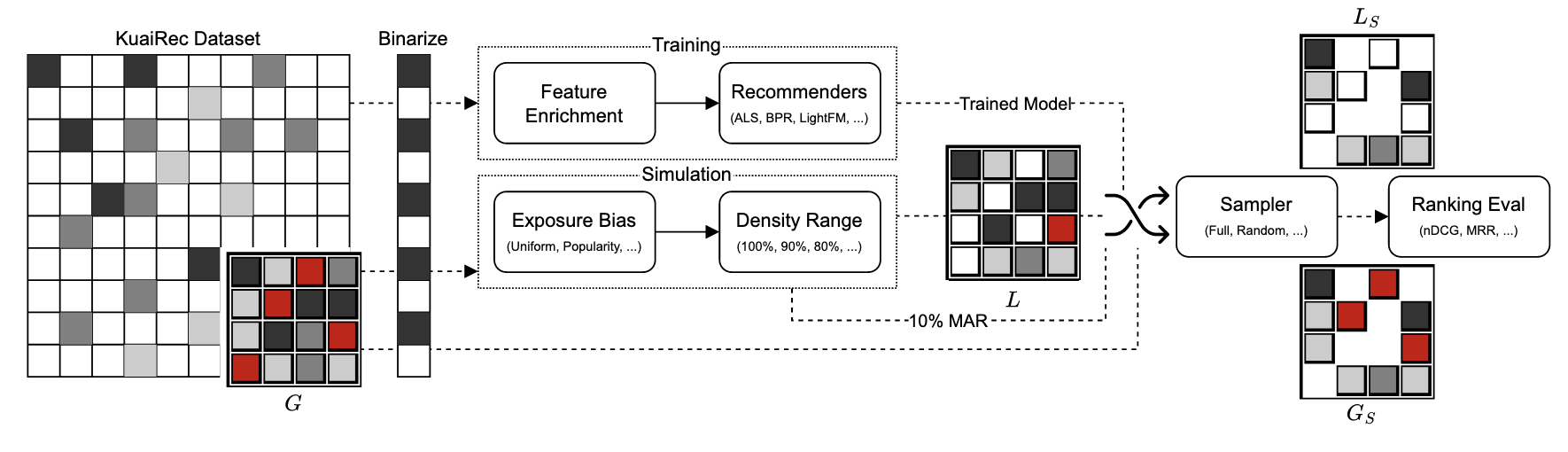
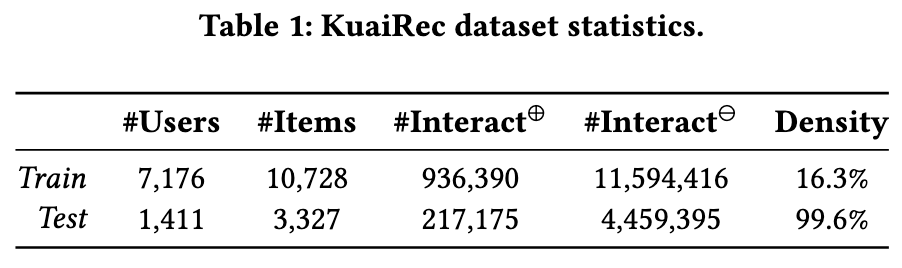
• 为了解答上述的问题, 作者在 KuaiRec 数据集上进行模拟 (KuaiRec 的测试集是一个几乎完全接近 $G$ 的数据集).

• (Logger) 为了模拟 Exposure Bias, 作者采用如下三种方式:

  1. Uniform: 每个 item 的曝光机会均等, 即没有 exposure bias 的情况;
  2. Popularity-biased: item 的曝光机会与其流行度成正比;
  3. Positivity-biased: item 的曝光机会与其作为正反馈的数量成正比.

• (Sparsity) 上述的 Logger 会采样多个 level 的 sparsity 的 $L$, 从 0% 到 95%.

• (Sampler) 下面只有 @$n$ 的 sampler 的结果是受采样大小影响的:

  1. Full: 所有 non-positive (非 ‘1’) 的交互均作为负样本;
  2. Exposed: 所有 negative (‘0’) 的交互 Item 作为负样本;
  3. Random@$e$: 均匀采样 $e$ 个 non-positive 的 Item, $e$ 等于该 user 的观测到的 negative (‘0’) 的数量;
  4. Random@$n$: 均匀采样 $n$ 个 non-positive 的 Item;
  5. Popularity@$n$: 依照流行度 (Zipf’s law) 采样 $n$ 个 non-positive 的 Item;
  6. Positivity@$n$: 依照正样本率 (Zipf’s law) 采样 $n$ 个 non-positive 的 Item;
  7. WTD@$n$: samples $n$ non-positives weighted based on empirical exposure distributions;
  8. WTDH@$n$: heuristic version of WTD with uniform exposure assumptions;
  9. Skew@$n$: samples $n$ non-positives, with selection probabilities defined by empirical popularity distributions.

• (Models) ALS, BPR, LightFM, SAR-Cosine, SAR-Jaccard, Popularity, Random.

比较实验

Resolution

• (考察点) 不同 Sampler 下的不同方式对于模型区分度如何?

• (衡量指标) 作者采用 Tie rate 来衡量区分度, 它定义为两个模型对一个用户的 NDCG@100 指标相同的比率, 越高说明区分度越差.

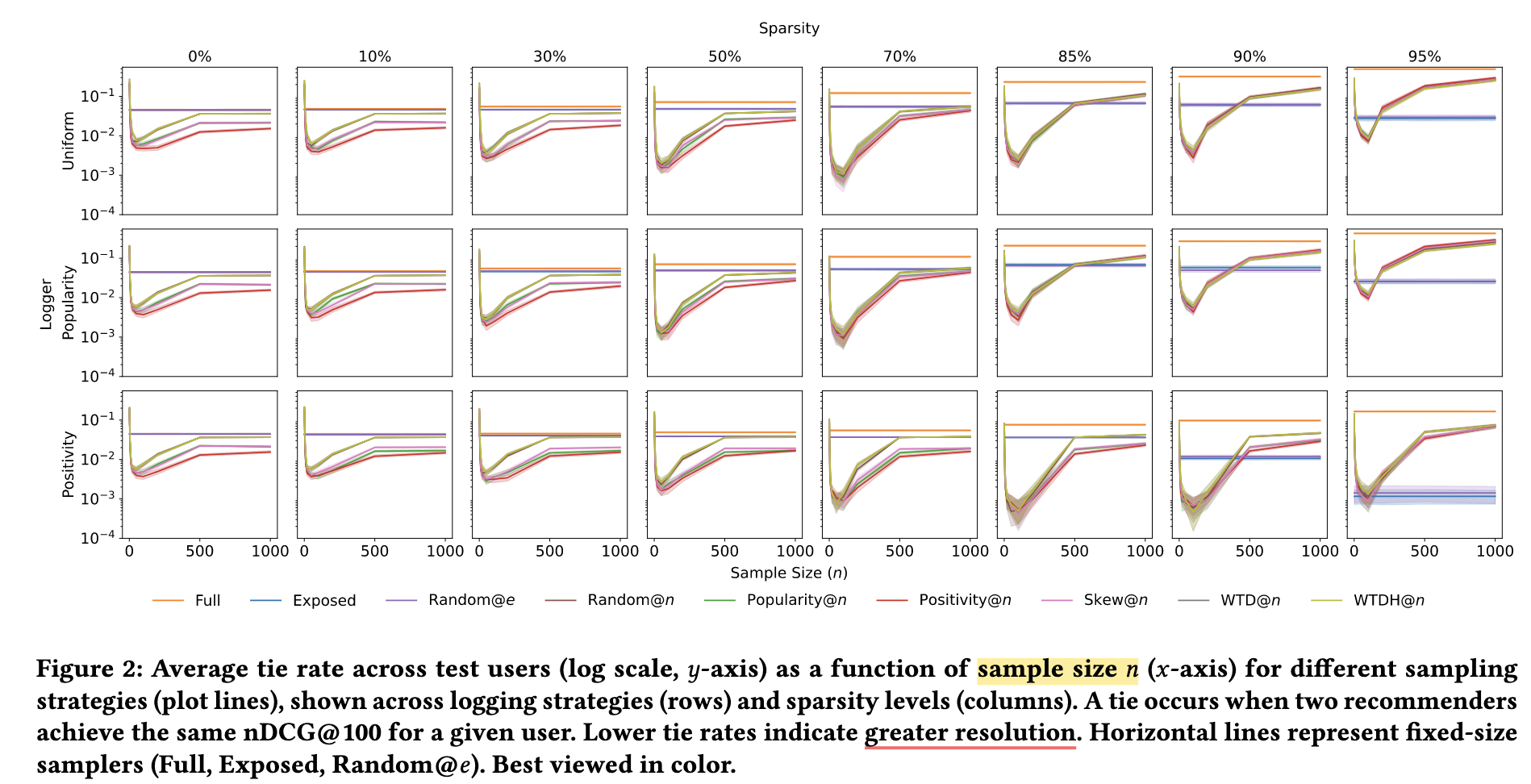
• (结论)
  1. 大部分 Sampler 的最佳区分度在一个较小的 $n$ 上取得;
  2. 随着 $L_S$ 的越发稀疏, Full Ranking 的区分度越来越差, 其他 Sampler 则视 Logger 而定.

注: 个人认为, Resolution 这个评价指标可能有失偏颇, 因为 full ranking 区分度差大体上是因为太难了, 可能导致很多 model 都给出一个偏差的结果.

Fidelity

• (考察点) 不同 Sampler 在 $L_S, L$ 上的评价是否一致, 实际上就是评估 sampled-based ranking 和 full ranking 的一致性.

• (衡量指标) 作者采用 Kendall’s $\tau$ 来衡量, 它定义为两个 ranking 序列的相关性, 越高说明越一致.

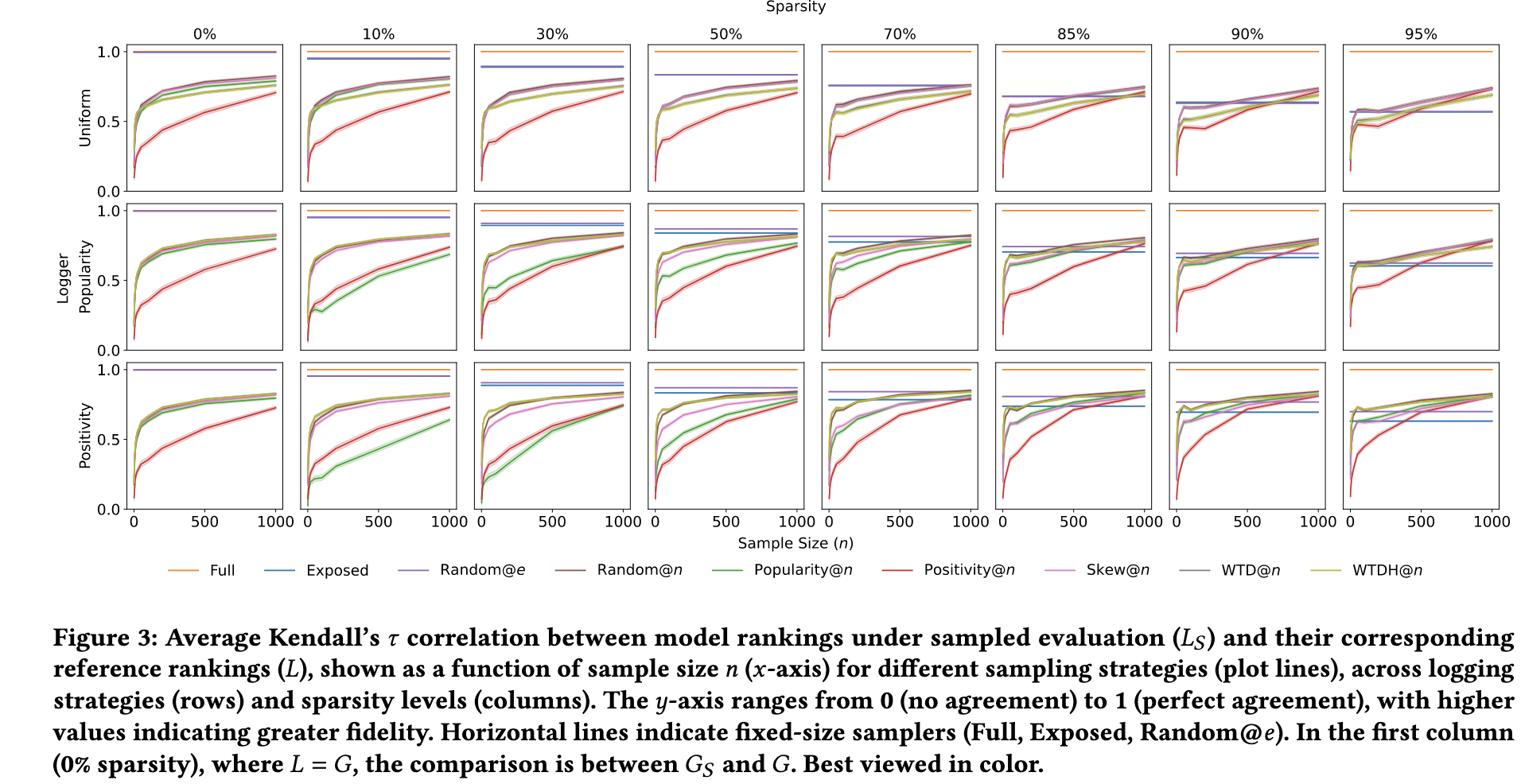
• (结论)
  1. 采样个数越多, 越一致;
  2. 但是, 即使是 0% sparsity 的情况下, 采样也不能完全逼近 full ranking.

Robustness

• (考察点) 不同 Sampler 在 $L_S, G_S$ 上的评价是否一致, 反映 sampling 带来的 bias.

• (衡量指标) 作者采用 Kendall’s $\tau$ 来衡量, 它定义为两个 ranking 序列的相关性, 越高说明越一致.

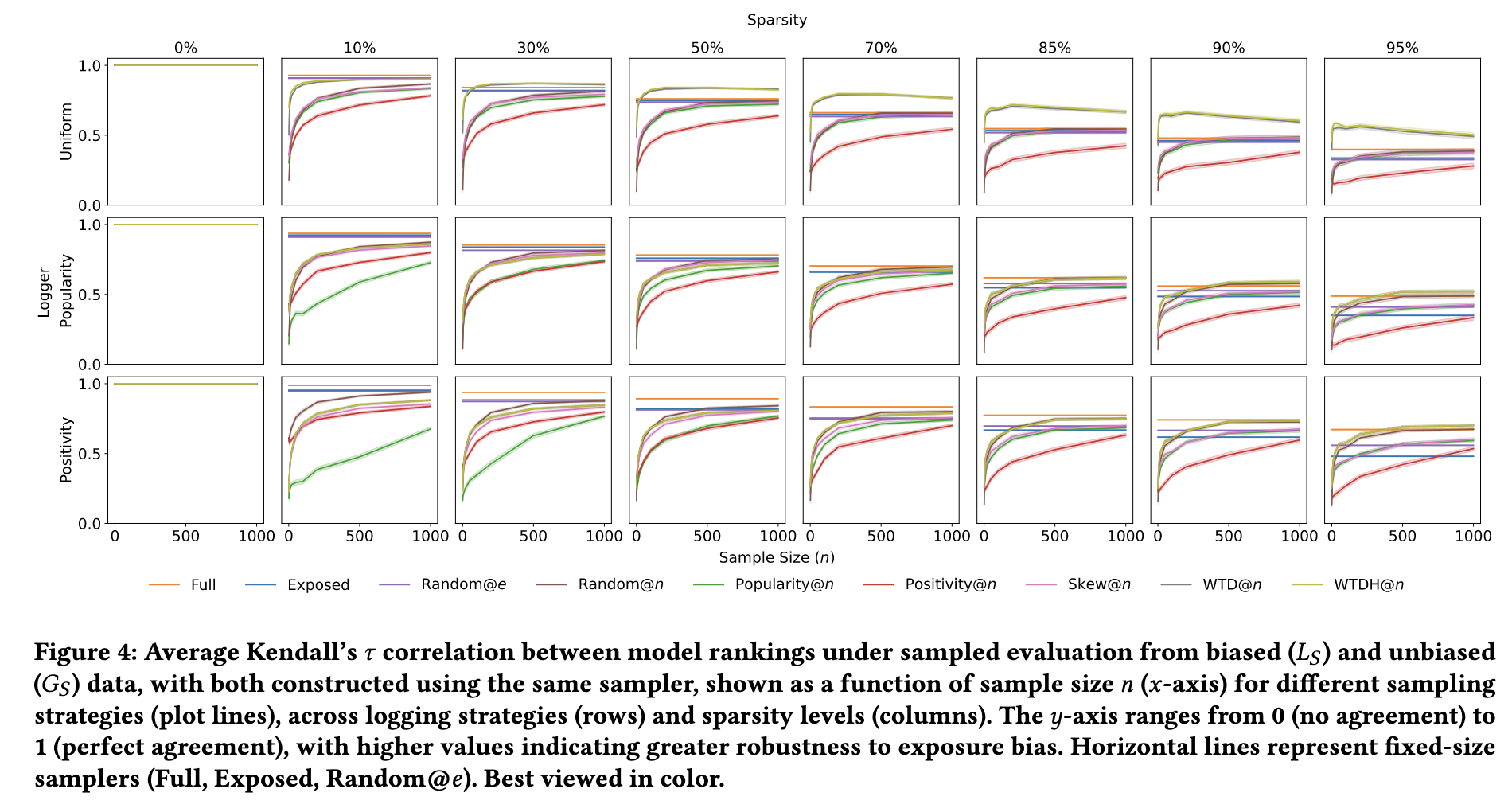
• (结论)
  1. WTD, WTDH 的效果在各个场景下基本上都是最好的.
  2. 通过增加 $n$, 很多 samplers 基本上都能和 full ranking 持平;
  3. Popularity 在稀疏度较低的情况下效果还行, 而 positivity 则相反.

Predictive Power

• (考察点) 不同 Sampler 在 $L_S, G$ 上的评价是否一致, 反映 sampling 带来的 bias 和 exposure bias.

• (衡量指标) 作者采用 Kendall’s $\tau$ 来衡量, 它定义为两个 ranking 序列的相关性, 越高说明越一致.

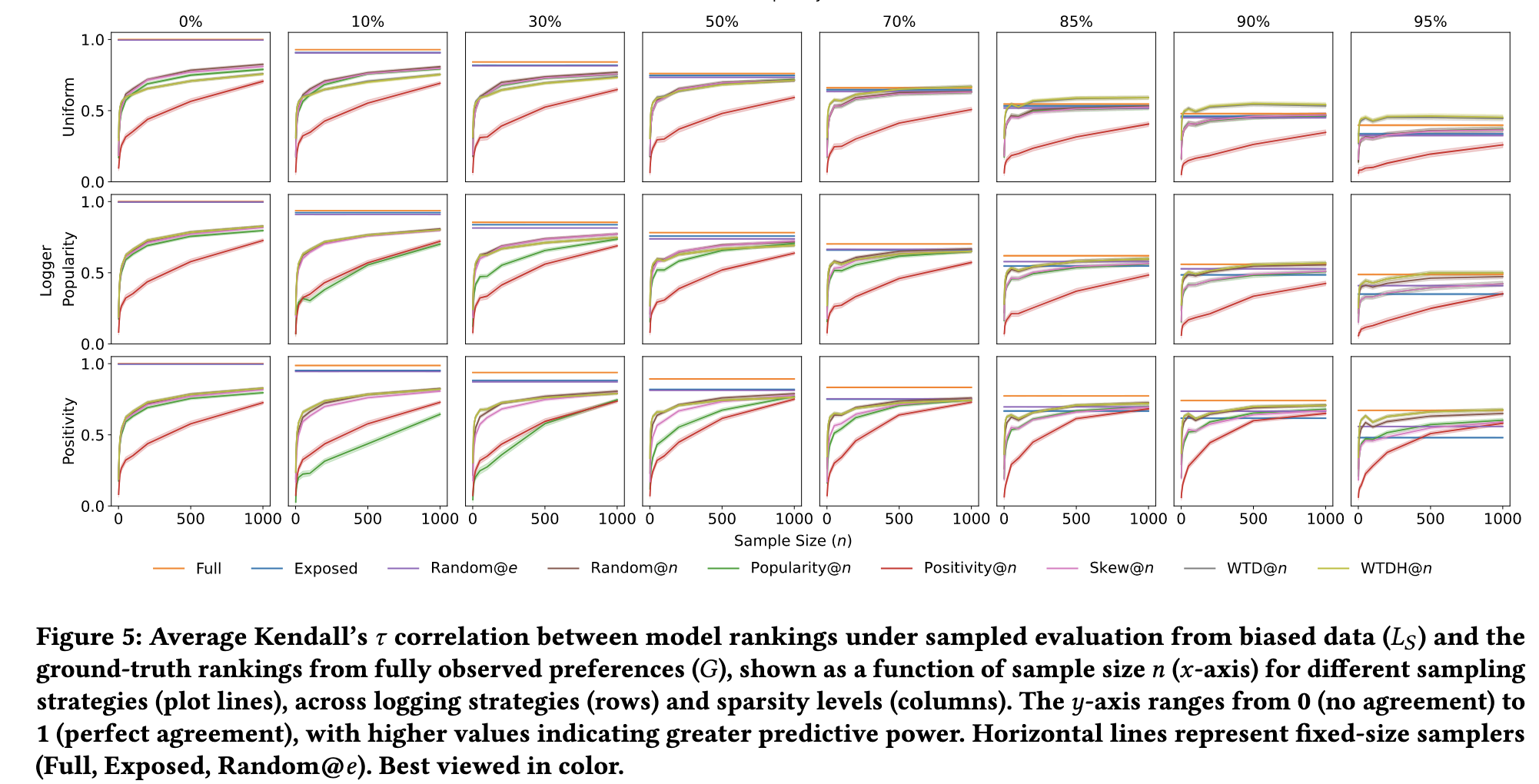
• (结论)
  1. WTD, WTDH 的效果在各个场景下基本上都是最好的. Random 的效果虽然稍差, 但是考虑到他的简单, 已经是很让人欣喜了.

结论

• 如果不考虑所谓的区分度, full ranking 依旧是最好的选择. WTD, WTDH 等方法虽然通过增加 $n$ 可以媲美 full ranking, 但是这个时候也失去了所谓的区分度, 因此鱼和熊掌是不可兼得的 (实际上区分度, 个人感觉并不那么客观). 总而言之, 即想要效果, 又想要效率, 就需要去估计所谓的 exposure 分布 (不过 random 采样的效果也还可以接受). 不过可能不建议通过简单的诸如流行度等方法采样负样本.

参考文献

1. Krichene W. and Rendle S. On Sampled Metrics for Item Recommendation. KDD, 2020. [PDF] [Code]
2. Pereira B. L., Said A. and Santos R. L. T. On the Reliability of Sampling Strategies in Offline Recommender Evaluation. arXiv, 2025. [PDF] [Code]