Scaling Laws

预备知识

• (Scaling Laws) 现在模型的规模已经达到了百 B 甚至是千 B 的规模, 然而训练如此庞大规模的模型需要诸多考量: 需要多少 tokens 的数据, 模型的 Width, Depth, Hidden Size 的配比, 训练过程中 Batch Size, Learning Rate 的调节等等. Scaling Laws 主要就是刻画了模型大小和所需数据量的关系, 通过在小规模上的训练结果可以预测在更大规模上训练的效益. 虽然最早由 [1] 发现了此项规律, 但是 Scaling Law 的正式系统性的刻画由 [3] 完成, [4] 则是在此基础上进行了一些修正.

• (符号说明)

  • $N$: non-embedding parameters;
  • $B$: batch size;
  • $S$: optimization steps;
  • $D = B * S$: dataset size;
  • $L$: (test) cross-entropy loss;
  • $C \approx 6ND = 6NBS$, total non-embedding training compute.

• (Parameter and Compute Scaling of Transformers) 下表展示了 Transformer 的参数量以及 (forward) 计算量和一些超参数的关系 (假设 $d_{\text{attn}} = d_{\text{ff}} / 4 = d_{\text{model}}$):

  • $d_{\text{model}}$: embedding 维度;
  • $d_{\text{ff}}$: feed-forward 维度;
  • $d_{\text{attn}}$: attention 维度;
  • $n_{\text{layer}}$: 层数;
  • $n_{\text{heads}}$: 注意力头数目.

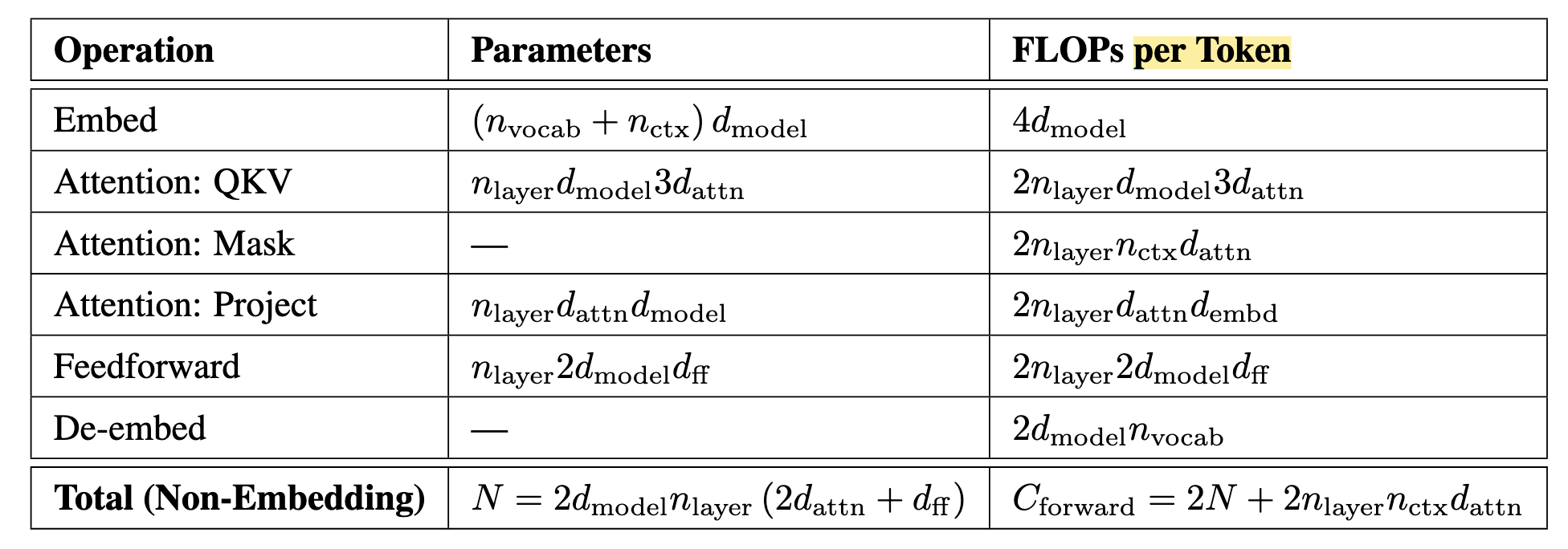
proof:

• (Attention):

  • QKV: 三个独立的变换矩阵 $W \in \mathbb{R}^{d_{\text{model}} \times d_{\text{attn}}}$, 因此共有 $n_{\text{layers}} \times 3 \times d_{\text{model}} \times d_{\text{attn}}$ 的参数量, 这里只涉及到矩阵乘法 ($\bm{e}W$ 需要 $2 \times d_{\text{model}} \times d_{\text{attn}}$ 量级的乘加运算), 总共 $2 \times n_{\text{layers}} \times 3 \times d_{\text{model}} \times d_{\text{attn}}$.

  • Mask: 这部分主要是每个 token 和其他 tokens 的交互.

  • Project: 包含 1 个独立的变换矩阵 $W \in \mathbb{R}^{d_{\text{attn}} \times d_{\text{model}}}$, 因此所对应的参数量和计算量是 QKV 阶段的 1/3.

• (Feedforward) FFN 一般由两个线性层组成 $W_{\text{up}} \in \mathbb{R}^{d_{\text{model}} \times d_{\text{ff}}}, W_{\text{down}} \in \mathbb{R}^{d_{\text{ff}} \times d_{\text{model}}}$, 容易证明参数量和计算量如上表所示.

• 因此, 倘若 $n_{\text{ctx}}$ (context) 不太长, 前向的计算量基本上 $2N$ per token 级别. 另外 $4N$ 来自于反向传播的开销, 注意到:

  $$ \underbrace{\bm{y}}_{1 \times m} = \underbrace{\bm{x}}_{1 \times n} \underbrace{\bm{W}}_{n \times m} \longrightarrow \nabla_{\bm{x}} \mathcal{L} = \nabla_{\bm{y}} \mathcal{L} \cdot W^T, \: \nabla_{W} \mathcal{L} = \bm{x}^T \nabla_{\bm{y}} \mathcal{L}. $$

  计算 $W$ 上的梯度和用于后续链式传播的 $\nabla_{\bm{x}}\mathcal{L}$ 都需要 $m \times n$ 的计算量, 因此反向传播消耗的计算量是前向的两倍.

• 因此, 总的计算量大抵是 $C \approx 6ND$.

核心思想

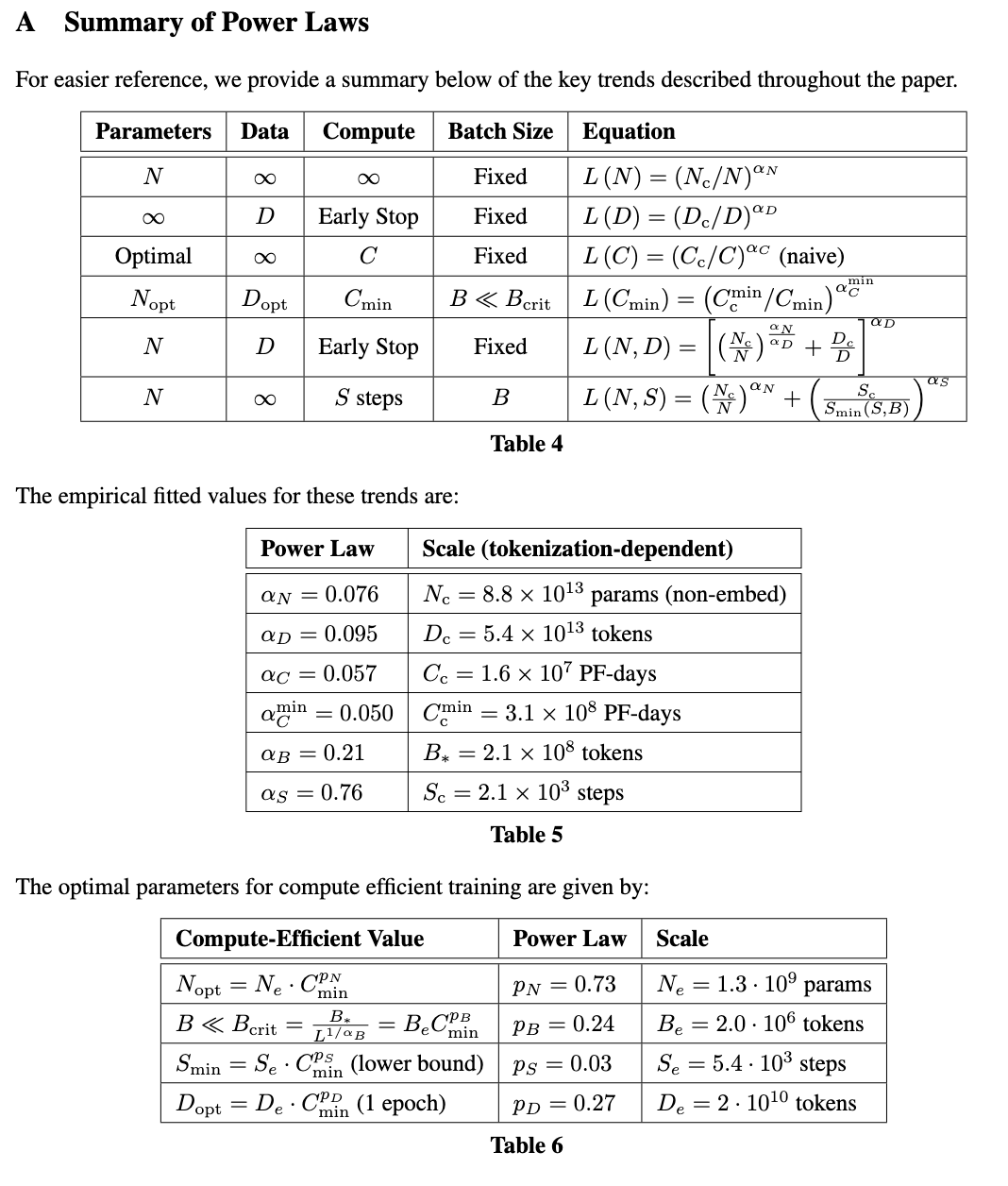
• Scaling Laws 的意义在于给定额定的计算量 $C$ 我们可以找到模型参数量 $N$ 和训练数据量 $D$ 的最优搭配, 即

  $$ N_{\text{opt}}(C), D_{\text{opt}}(C) = \mathop{\text{argmin}} \limits_{N, D \: \text{s.t.} \text{FLOPs}(N, D) = C} L(N, D). $$

• (L-N-D Scaling Law) 作者假设 $L, N, D$ 满足如下的关系:

  $$ \tag{L-N-D} L(N, D) = \left(\frac{N_c}{N}\right)^{\alpha_N} +\left(\frac{D_c}{D}\right)^{\alpha_D}, $$

  这里 ($N_c, D_c, \alpha_N, \alpha_D$) 都是需要通过数据拟合的值. 这种参数化除了比较贴合实际的观测数据外, 同时符合一些必要的性质:

  1. 一般来说, 随着词表大小的改变, $L$ 也会相应的改变, $N_c, D_c$ 的存在可以很好的适应这一点;
  2. 固定 $N$, 当 $D \rightarrow \infty$ 的时候 $L(N, D) \rightarrow L(N)$, 而根据实验观察 (见下图) 确实 $L(N)$ 的幂律形式确实拟合的很好, 反之亦然.

• 注意 Figure 1 的横坐标和纵坐标都是对数化过的: 倘若 $y = c \cdot x^{\alpha}$, 对数化后:

  $$ \log y = \log c + \alpha \cdot \log x, $$

  即 $(\log y, \log x)$ 之间满足的是线性关系.

• $D = B S$, 但是是否对于任意组合的 $(B, S)$ 都满足 (L-N-D) 呢? 显然不是. [2] 中指出:

  • 存在 critical batch size $B_{\text{crit}}(L)$, 在 $B < B_{\text{crit}}$ 的条件下, 增加 $B$ 可以在相同计算成本 $C$ 下取得相近的收敛结果 $L$;
  • 一旦 $B > B_{\text{crit}}$, 继续增加 Batch Size 虽然可以进一步减少收敛到 $L$ 所需的迭代次数 $S$, 然而所需总的计算量是增加的.

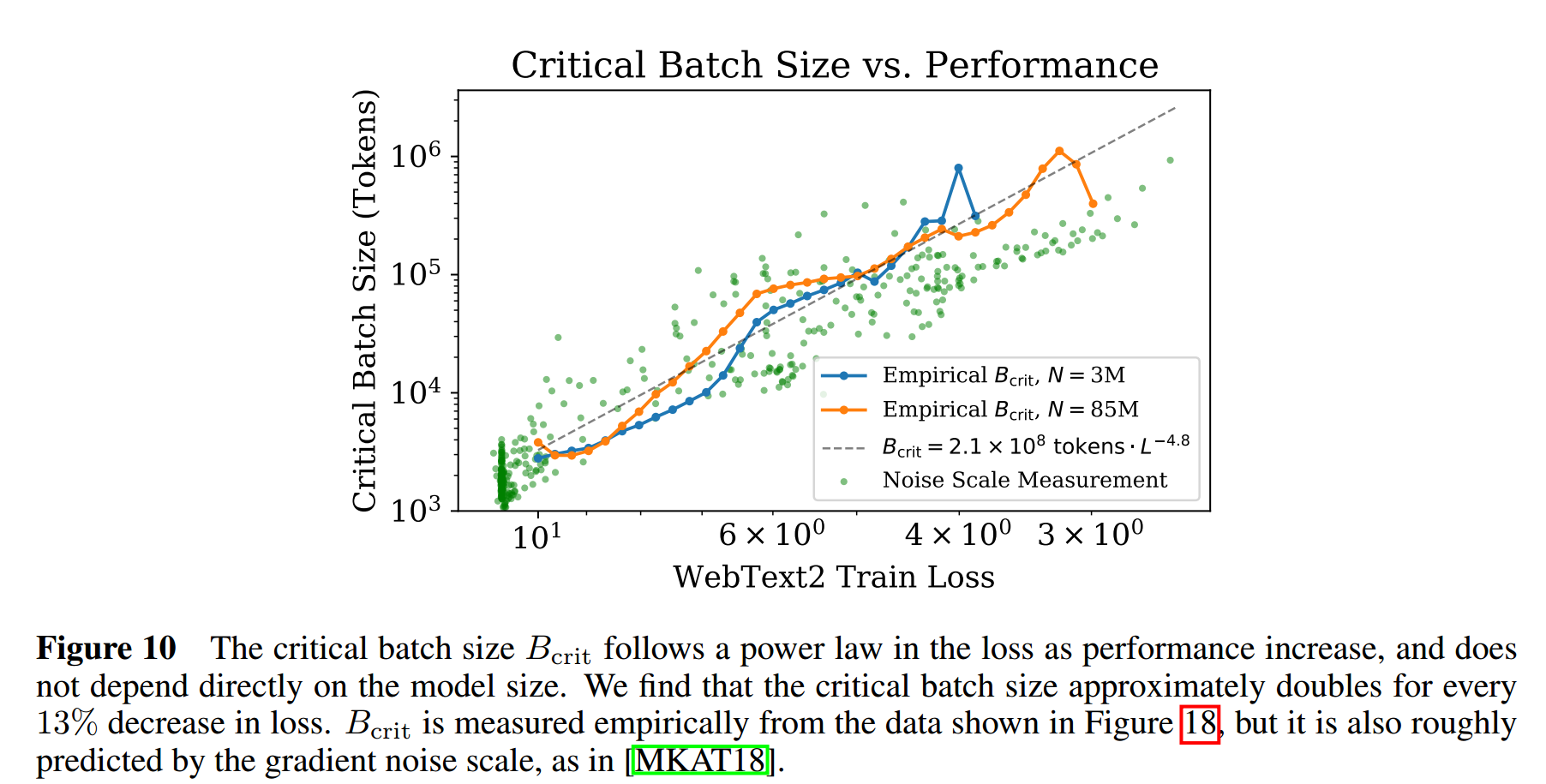
• (L-B Scaling Law) 特别地, 通过上图可以发现:

  $$ \tag{L-B} B_{\text{crit}}(L) \approx \frac{B_*}{L^{1 / \alpha_B}}, \quad B_* \approx 2 \times 10^8, \alpha_B \approx 0.21. $$

• 假设 $S_{\min}(L)$ 是使用 $B_{\text{crit}}(L)$ 所需的最少的迭代次数, 采用另一套同样能收敛到 $L$ 的训练策略 ($B, S$) 满足${}^{[2]}$

  $$ \tag{B-S} \left( \frac{S}{S_{\min}} - 1 \right) \left( \frac{D}{D_{\min}} - 1 \right) = 1, \\ D = BS, \quad D_{\min} = B_{\text{crit}} \cdot S_{\min}. $$

  通过一定的变换, 我们有

  $$ S_{\min}(S) = \frac{S}{1 + B_{\text{crit}}(L) / B} \\ \Rightarrow S_{\min}(S) = \frac{D}{B + B_{\text{crit}}(L)} \\ \Rightarrow D_{\min}(D) = \frac{D}{B / B_{\text{crit}}(L) + 1} \\ \Rightarrow C_{\min}(C) = \frac{C}{B/B_{\text{crit}}(L) + 1}. $$

• (L-N-S Scaling Law) 代入 (L-N-D) 的关系, 我们有 (L-N-S) 的关系

  $$ \tag{L-N-S} L(N, S_{\min}) = \left( \frac{N_c}{N} \right)^{\alpha_N} +\left( \frac{S_c}{S_{\min}} \right)^{\alpha_S}. $$

• 接下来, 让我们借助上面预设的关系继续推导 (L-C), (N-C), (S-C), (B-C).

• 结合 (L-N-S) 和 (B-S) 以及 $C = 6NBS$, 我们有:

  $$ \tag{L-N-C} L(N, C) = \left( \frac{N_c}{N} \right)^{\alpha_N} +\left( 6B_* S_c \frac{N}{ L^{1/\alpha_B} C } \right)^{\alpha_S}. $$

  通过令 $\partial_N L|_C = 0$, 我们可以找到最优条件:

  $$ \begin{align*} 0 &= \partial_N L|_C \\ &= -\frac{\alpha_N}{N} \left( \frac{N_c}{N} \right)^{\alpha_N} +\frac{\alpha_S}{N}\left( 6B_* S_c \frac{N}{L^{1 / \alpha_B} C} \right)^{\alpha_S} \left( 1 - \frac{N}{\alpha_B L} \underbrace{\frac{\partial L}{\partial N}|_C}_{=0} \right) \\ \Rightarrow \frac{\alpha_N}{\alpha_S} \left( \frac{N_c}{N} \right)^{\alpha_N} &= \left( 6B_* S_c \frac{N}{L^{1 / \alpha_B} C} \right)^{\alpha_S} \\ \Rightarrow (N_{\text{eff}})^{\alpha_N + \alpha_S} &\propto L^{\frac{\alpha_S}{\alpha_B}} C^{\alpha_S}. \end{align*} $$

• (L-C Scaling Law)这里, $N_{\text{eff}}$ 表示 $C$ 下的最优参数量. 将其代入 (L-N-C) 可得

  $$ L(N_{\text{eff}}(C), C) = \left( 1 + \frac{\alpha_N}{\alpha_S} \right) L(N_{\text{eff}}, \infty), $$

  通过整理, 我们有

  $$ \tag{L-C} L(C) = \left(\frac{C_c}{C}\right)^{\alpha_C}, \\ \alpha_C = \frac{1}{1 / \alpha_N + 1 / \alpha_B + 1 / \alpha_S}, \quad C_c = 6N_c B_* S_c \left( 1 + \frac{\alpha_N}{\alpha_S} \right)^{1 / \alpha_S + 1 / \alpha_N} \left( \frac{\alpha_S}{\alpha_N} \right)^{1 / \alpha_S}. $$

• (N-C Scaling Law) 类似地, 通过把 $L$ 替换掉, 我们有

  $$ \tag{N-C} N(C) = N_c \left( \frac{C}{C_c} \right)^{\alpha_C / \alpha_N} \left( 1 + \frac{\alpha_N}{\alpha_S} \right)^{1 / \alpha_N}. $$

• (S-C Scaling Law) 类似地,

  $$ \tag{S-C} S(C) = \frac{C_c}{6N_c B_*} \left( \frac{C}{C_c} \right)^{\alpha_C / \alpha_S} \left( 1 + \frac{\alpha_N}{\alpha_S} \right)^{-1 / \alpha_N}. $$

• (B-C Scaling Law) 类似地,

  $$ \tag{B-C} B(C) = B_* \left( \frac{C}{C_c} \right)^{\alpha_B / \alpha_S}. $$

• 因此, 原则上只要我们有了 (L-N-S) 和 (L-S), 就能推导出其他的 scaling laws 了. 当然我们也可以对每一个 Scaling Law 进行估计, 作者通过两种方式得到的结果相差不大.

• (注) 根据最开始的表, 我们发现:

  $$ \alpha_C / \alpha_N \approx 0.68, \: \alpha_C / \alpha_B \approx 0.25, \alpha_C / \alpha_S \approx 0.07. $$

  因此, $N(C) \propto C^{0.68}, D(C) = B(C) \cdot S(C) \propto C^{0.32}$, 得出的结论是模型的 scaling 速度要比数据快一点. 但是 [4] 进行了更大规模的实验后发现, 实际上应该

  $$ N(C) \propto C^{0.5}, \quad D(C) \propto C^{0.5}. $$

(L-N-D) Scaling Law 用于 Overfitting 判断

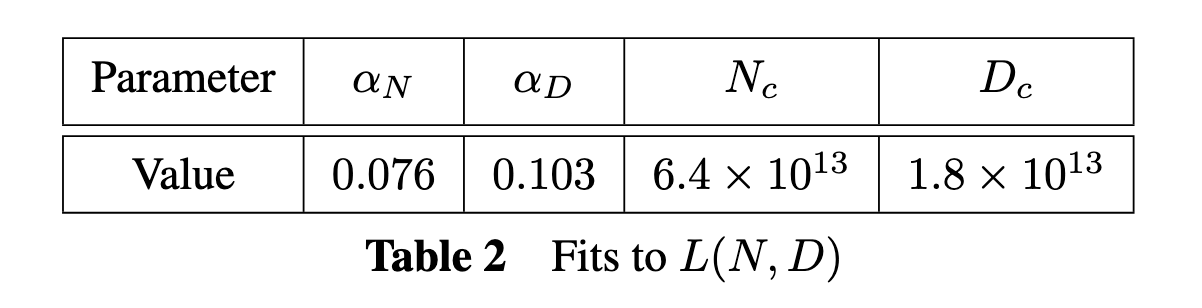
• 假设 (L-N-D) 的拟合值如上, 如何借助 $L(N, D)$ 来判断需要多少数据来避免 Overfitting?

• 我们通常采用如下指标来判断是否过拟合:

  $$ \delta L(N, D) := \frac{L(N, D)}{L(N, \infty)} - 1. $$

  即当前的 loss 和最理想的情况 $L(N, \infty)$ 的比较. 假设当 $\delta L(N, D) > 0.02$ 的时候, 我们认为模型已经过拟合了. 即避免过拟合要求

  $$ \delta L(N, D) := \frac{L(N, D)}{L(N, \infty)} - 1 \le 0.02 \\ \Rightarrow \frac{ \left( \frac{6.4 \times 10^{13}}{N} \right)^{0.076} +\left( \frac{1.8 \times 10^{13}}{D} \right)^{0.103} }{ \left( \frac{6.4 \times 10^{13}}{N} \right)^{0.076} } \le 0.02 \\ \Rightarrow D \gtrapprox (5 \times 10^3) N^{0.74}. $$

(L-N-D) Scaling Law 用于早停判断

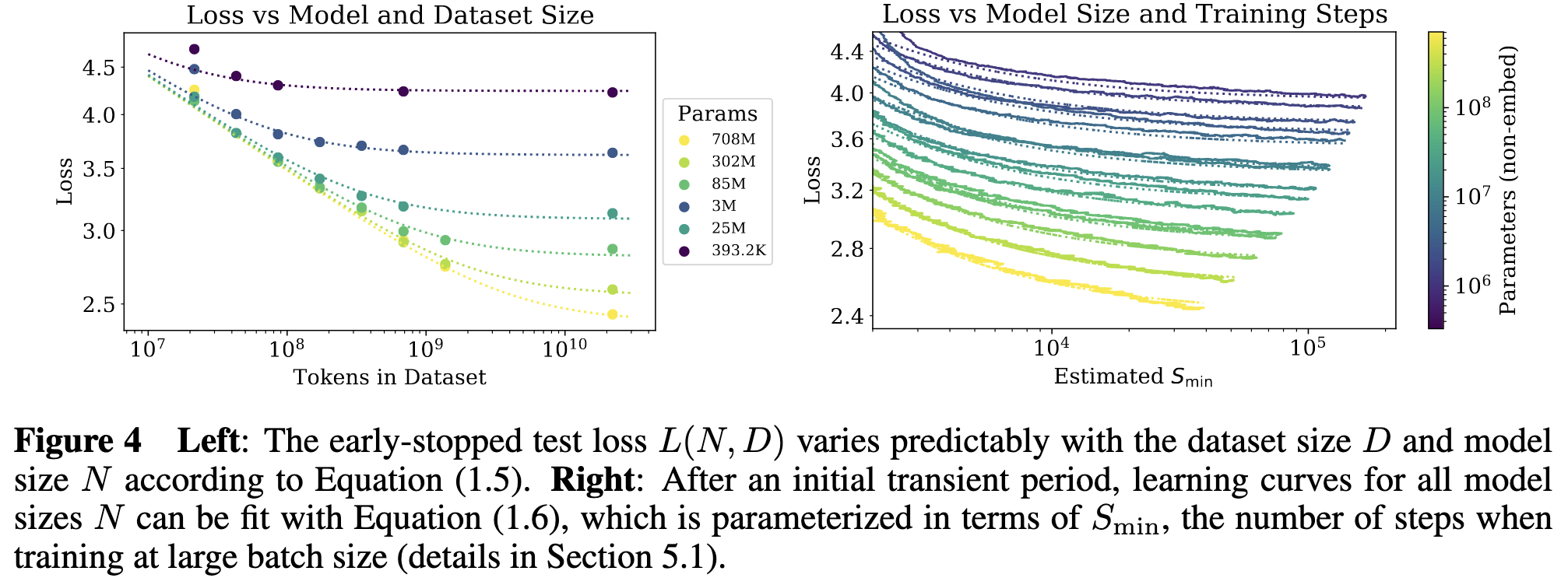
• $S_{\min}$ 实际上给了一个很好的早停 steps 的估计, 通过 (L-N-S) 的关系式, 我们可以得到如下的关系:

  $$ L(N, D) = L(N, S_{\min}) = \underbrace{ \left( \frac{N_c}{N} \right)^{\alpha_N} }_{L(N, \infty)} +\left( \frac{S_c}{S_{\min}} \right)^{\alpha_S} \\ \Rightarrow S_{\text{stop}}(N, D) \gtrapprox S_{\min} = \frac{S_c}{ [L(N, D) - L(N, \infty)]^{1 / \alpha_S} }. $$

参考文献

1. Hestness J., Narang S., Ardalani N., Diamos G., Jun H., Kianinejad H., Patwary M. M. A., Yang Y. and Zhou Y. Deep Learning Scaling is Predictable, Empirically. arXiv, 2017. [PDF] [Code]
2. McCandlish S., Kaplan J., Dario A., and OpenAI Dota Team. An Empirical Model of Large-Batch Training. arXiv, 2018. [PDF] [Code]
3. Kaplan J., McCandlish S., Henighan T., Brown T. B., Chess B., Child R., Gray S., Radford A., Wu J. and Amodei D. Scaling Laws for Neural Language Models. arXiv, 2020. [PDF] [Code]
4. Hoffmann J., Borgeaud S., Mensch A., Buchatskaya E., Cai T., Rutherford E., de Las Casas D., Hendricks L. A., Welbl J., Clark A., Hennigan T., Noland E., Millican K., van den Driessche G., Damoc B., Guy A., Osindero S., Simonyan K., Elsen E., Rae J. W., Vinyals O. and Sifre L. Training Compute-Optimal Large Language Models. arXiv, 2022. [PDF] [Code]