Addressing Representation Collapse in Vector Quantized Models with One Linear Layer
预备知识
- 请先了解 VQ-VAE 的相关背景.
核心思想
向量量化主要是将隐向量 $\bm{z} \in \mathbb{R}^{d}$ 映射为离散 token 过程. 实际上为从 Codebook $\mathcal{C} = \{\bm{c}_1, \bm{c}_2, \ldots, \bm{c}_K\}$ 的过程, 通常是通过如下的过程实现:
$$ \bm{q} = \text{argmin}_{\bm{c} \in \mathcal{C}} \| \bm{z} - \bm{c}\|_2^2. $$容易发现, 这个操作是没法将 $\bm{q}$ 上的梯度传回至 $\bm{e}$ 的. 因此, 为了保证 Encoder 的顺利训练, 我们通常运用 straight-through estimator (STE):
$$ \bm{q} \leftarrow \bm{e} + (\bm{q} - \bm{e}), $$此时, 我们有 (假设 $\bm{e} \rightarrow \bm{q} \rightarrow \mathcal{L}$ 是前向传播的唯一路径):
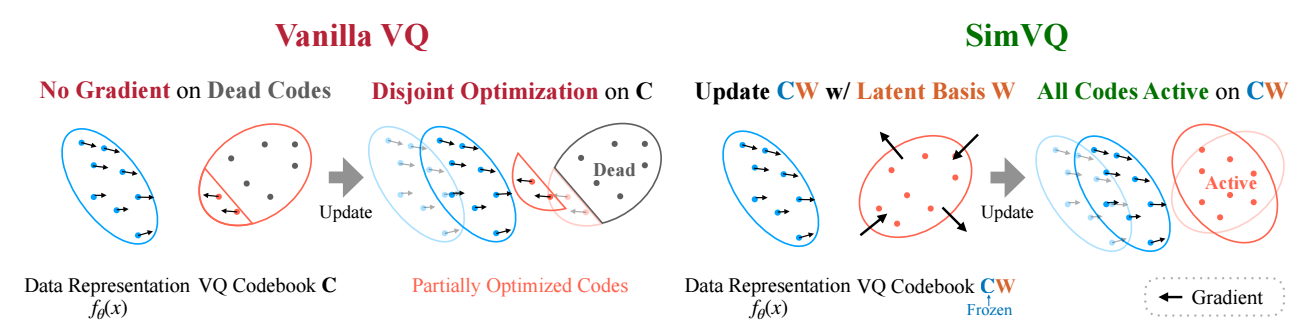
$$ \nabla_{\bm{e}} \mathcal{L} = \nabla_{\bm{q}} \mathcal{L}. $$然而即便如此, codebook collapse 依旧不可避免地发生了, 其主要问题在于在训练过程中 codebook 中很大一部分向量是难以得到充分训练的: 既然, 向量 $\bm{c}$ 得到训练当且仅当它匹配到部分 $\bm{z}$.
SimVQ
SimVQ 的做法很简单, 利用高斯分布初始化一个 $K \times d$ 的 codebook 矩阵 $C \in \mathbb{R}^{K \times d}$ 并固定它. 然后引入一个可学习的矩阵 $W \in \mathbb{R}^{d \times d}$, 最终的 codebook 为
$$ C W \Leftrightarrow \{W^T\bm{c}_1, W^T\bm{c}_2, \ldots, W^T \bm{c}_K\}. $$注意到, 此时任意匹配都会引起 $W$ 的更新, 而 $W$ 的更新会间接导致 $\mathbf{W}^T \bm{c}$ 的改变. 因此, 作者认为此时就不会再有上面的训练不充分的问题了.