An Image is Worth 32 Tokens for Reconstruction and Generation
预备知识
- 对 VQ-VAE 有基本的了解.
核心思想
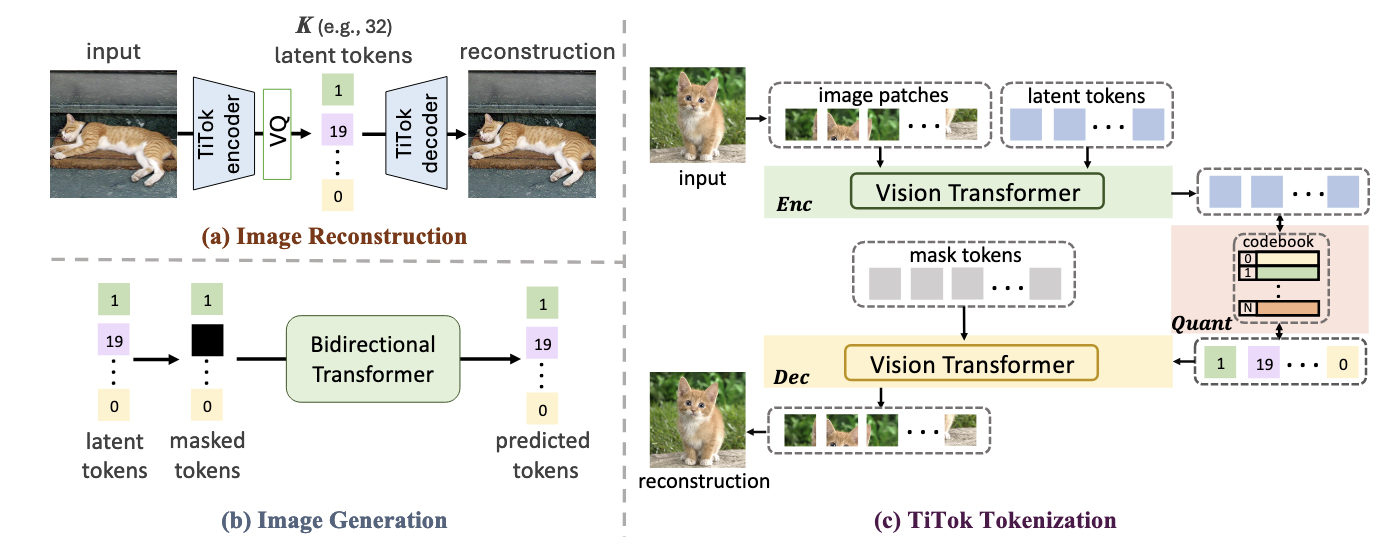
将图片压缩为一组 Visual Tokens 已经渐渐成为了主流 (由于其可以方便地和 LLM 等生成式模型结合).
然后, 以往的量化方法多半保留图片的结构性, 即图片 $\mathbf{I} \in \mathbb{R}^{H \times W \times 3}$ 首先 patch-wise 地’下采样’为 $\mathbf{Z} \in \mathbb{R}^{\frac{H}{f} \times \frac{W}{f} \times D}$, 例如 $f=16$ 通常是一个常见的选择, 此时 16x16 大小的 patch 对应一个 visual token.
作者认为, 这种方式阻碍了进一步提高压缩比. 过于强调 patch 的独立性反而难以编码图片中的主要信息, 从而导致 Visual Tokens 本身就存在了很大的冗余. 因此过往的方法通常需要 128/256 tokens per Image, 难以进一步提高压缩率.
(Encoding) TiTok 直接将 Image 按照 patch 展开得到 $\mathbf{P}$, 拼接 $K$ 个 learnable tokens $\mathbf{L} \in \mathbb{R}^{K \times D}$ 然后喂入 ViT 中. 其目的是希望这 $K$ 个 learnable tokens 不需要满足所谓的结构性, 逐步通过 Transformer 吸收图片的主要信息:
$$ \mathbf{Z} \in \mathbb{R}^{K \times D} = Enc(\mathbf{P} \oplus \mathbf{L}). $$(Quantization) $K$ 个 learnable tokens 最终得到 $K$ 个 latent tokens, 通过一般的向量量化方法即可得到离散编码.
(Decoding) 是在离散编码的基础上, 配合重复的 [mask] tokens, 来重建一个一个 Patch:
$$ \mathbf{\hat{I}} = Dec(Quant(\mathbf{Z}) \oplus \mathbf{M}), $$其中 $\mathbf{M} \in \mathbb{R}^{\frac{H}{f} \times \frac{W}{f} \times D}$.