Visual Autoregressive Modeling: Scalable Image Generation via Next-Scale Prediction
预备知识
- 请务必了解 VQGAN.
核心思想
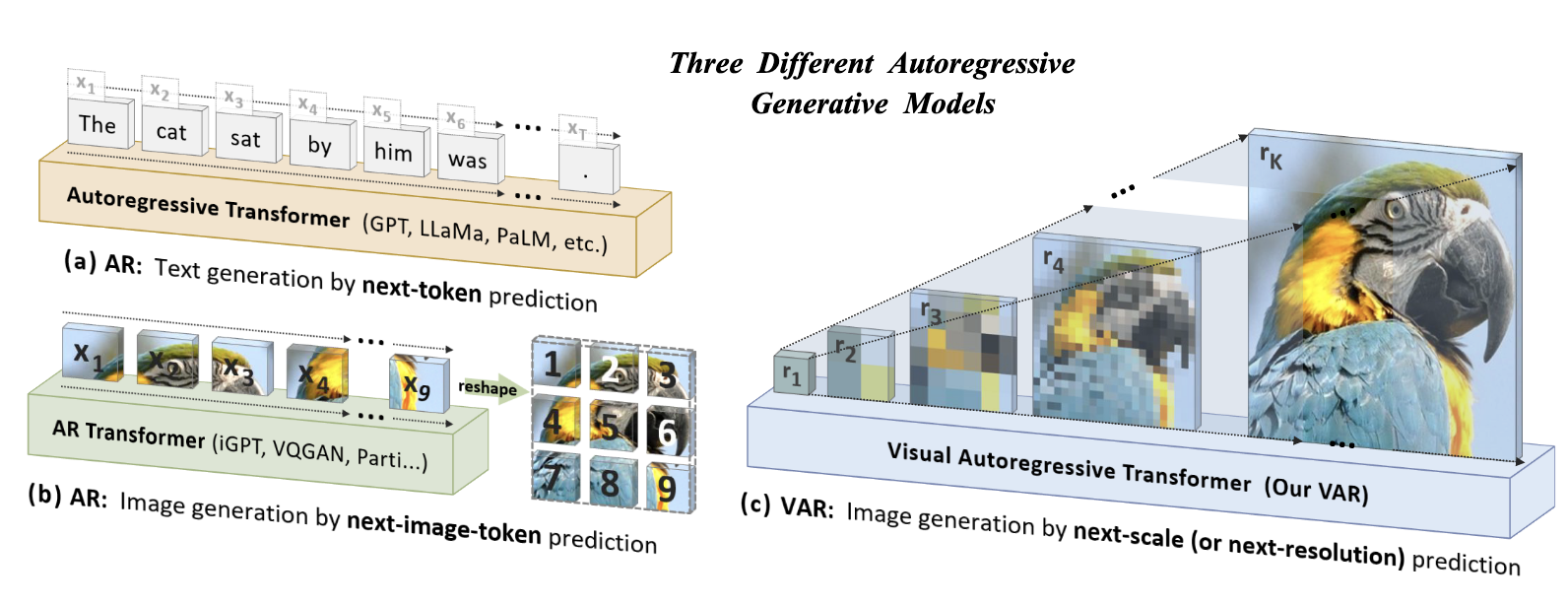
以往的图像自回归生成方法通常按照 row-by-row 的方式进行, 存在以下问题:
- 结构上的退化: 显然, row-by-row 的生成方式生硬地假设了后续的 Token 仅依赖前面的 Token 生成即可, 然而实际上一个 Token 和四周都有关系;
- 缺乏泛化性: 图像生成任务很多时候并不是简单的自回归形式能够一以贯之的, 比如在处理依赖后几行 pixels 恢复完整图像的时候, 现在的方法就难以胜任;
- 低效: 一个一个 Token 的自回归的生成是非常低效的.
此外, 如果 Token 是通过诸如 VQ-VAE 等方式得到的, Token 本身的构建就违背了自回归的假设.
Next-Scale Prediction
VAR 另辟蹊径, 采取 next-scale 的自回归生成方式:
$$ p(r_1, r_2, \ldots, r_K) = \prod_{k=1}^K p(r_k| r_1, r_2, \ldots, r_{K-1}). $$这里 $r_k \in [V]^{h_k \times w_k}$ 是一个尺度的 token 集合 (这些 token 通过类似 VQGAN 的方式得到).
例如, 我想要生成 256 x 256 大小的图案, 假设每 16个 pixel 大小的 patch 可以得到一个独立的 token, 即要求生成一个 16 x 16 tokens:
- 通过 prompt 生成 1 x 1 的 $r_1$;
- prompt + $r_1$ 生成 2 x 2 的 $r_2$;
- …
当然, 具体的 $h_k, w_k$ 可以自行设定.
到此可以发现, VAR 在结构上没有退化, 也具有很好的拓展性泛化性. 此外, VAR 的 attention mask 和一般的自回归方式不同, 每个 scale 内部的 token 是双向注意力, 而 $r_i, r_j$ 之间是自回归式的. 即一次 inference 我们就可以得到下一个 scale 所有的 tokens, 因此效率上也是大大提升了.
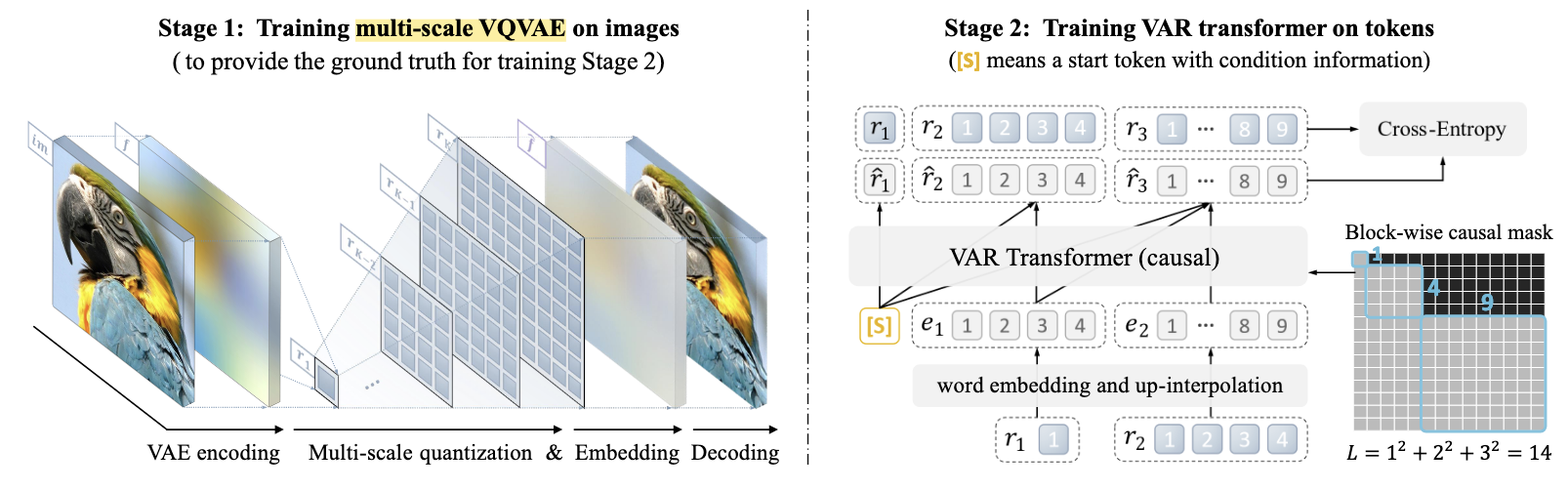
Multi-Scale Quantization

$\mathcal{E}$: Encoder; $\mathcal{Q}$: quantizer (返回离散编码); $\phi_k$ 额外的卷积层.
和一般的 VQ-VAE, VQ-GAN 不同, VAR 采取类似 RQ-VAE 的方式对不同的尺度进行离散编码.
如此一来, scale 和 scale 之间在构造时就天然满足自回归性质.
最后, 通过 VAR 得到的不同 scale 的预测结果, 通过 Decoder 可以’恢复’出图像.