Taming Transformers for High-Resolution Image Synthesis
预备知识
- 在学习 VQGAN 之前, 请务必先了解 VQ-VAE.
核心思想
- Transformer 已经在 NLP 领域取得了巨大的进展, 本文想要开发其在图像生成领域的能力.
Part1: 离散编码
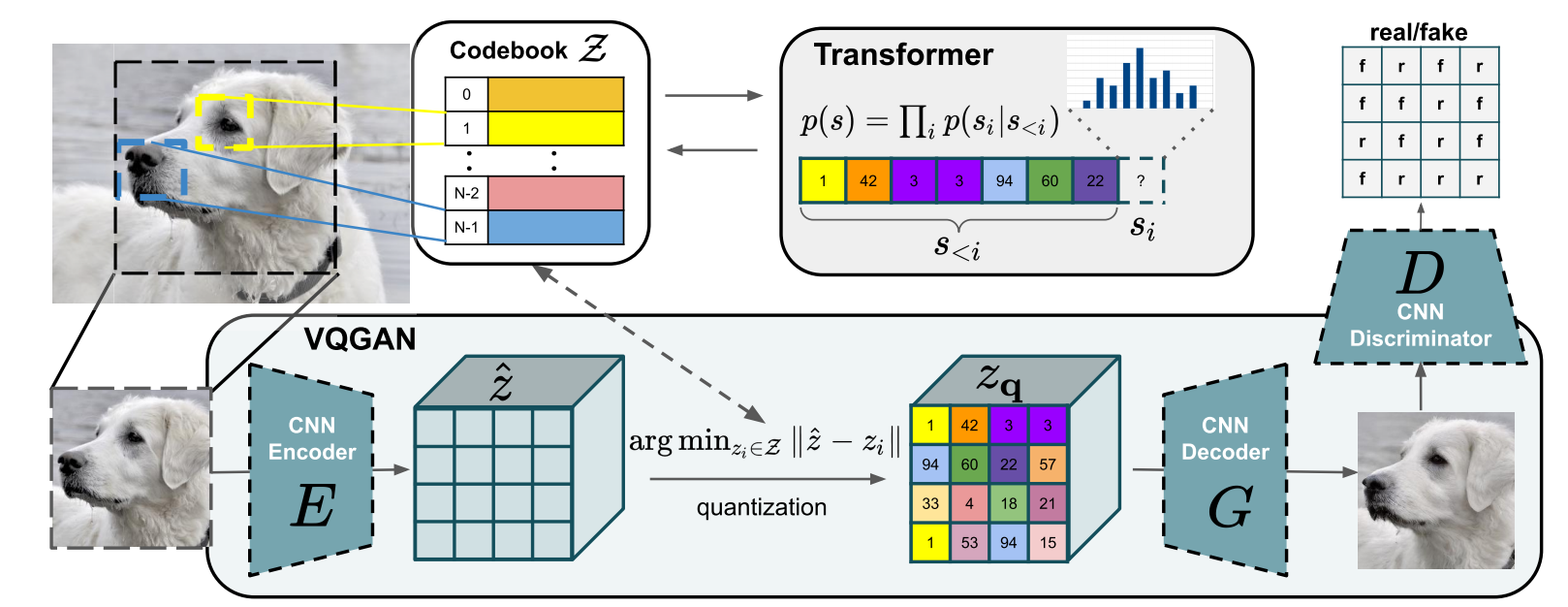
既然 Transformer 的成功依赖离散的 token, 那么通过它来生成图片很重要的一个点是如何将图片离散化? 于是乎, 作者引入了 VQGAN 来得到图片的离散编码.
给定一个图片 $x \in \mathbb{R}^{H \times W \times 3}$, 首先通过一个 CNN encoder $E$ 来得到初步的编码:
$$ \hat{z} = E(x) \in \mathbb{R}^{h \times w \times n_z}. $$接着, element-wise 地为每一个’像素点’匹配它的 token:
$$ z_{\mathbf{q}} = \mathbf{q}(\hat{z}) := \bigg(\text{argmin}_{z_k \in \mathcal{Z}} \|\hat{z}_{ij} - z_k\| \bigg)_{ij}, $$这里 $\mathcal{Z} = \{z_k\}_{k=1}^K \subset \mathbb{R}^{n_z}$, 俗称 codebook.
通过 CNN decoder, 我们可以还原出对应的图片:
$$ \hat{x} = G(z_{\mathbf{q}}). $$当然, 我们需要训练这个模型, 任务目标和 VQ-VAE 的略有不同:
$$ \mathcal{L} = \mathcal{L}_{VQ} + \lambda \mathcal{L}_{GAN}, \\ \mathcal{L}_{VQ} = \underbrace{\|x - \hat{x}\|^2}_{\mathcal{L}_{rec}} + \|\text{sg}(E(x)) - z_{\mathbf{q}} \|^2 + \|\text{sg}(z_{\mathbf{q}}) - E(x) \|^2, \\ \mathcal{L}_{GAN} = \log D(x) + \log (1 - D(\hat{x})). $$这里 $\text{sg}(\cdot)$ 表示梯度截断, $D(\cdot)$ 则是 GAN 里面常用的判别器. $\lambda$ 是一个自适应的超参数:
$$ \lambda = \frac{\nabla_{G_L} [\mathcal{L}_{rec}]}{\nabla_{G_L} \mathcal{L}_{GAN} + \delta}, $$这里 $\delta = 1e-6$ 是一个小量防止数值不稳定.
特别地, 文中有一句话:
To do so, we propose VQGAN, a variant of the original VQ-VAE, and use a discriminator and perceptual loss to keep good perceptual quality at increased compression rate.
- 因此, 实际使用的时候, $\mathcal{L}_{VQ}$ 中的 $\mathcal{L}_{rec}$ 应当替换为 perceptual loss.
Part2: Transformer 生成
通过上面我们就有了 $z_{\mathbf{q}}$, 它实际上可以表示为离散的 token:
$$ s \in \{0, \ldots, |\mathcal{Z}| - 1\}^{h \times w}, \quad s_{ij} = k \text{ such that } (z_{\mathbf{q}})_{ij} = z_k. $$因此, 我们可以把这些当成’文本’然后像一般的 NLP 那样进行 next-token predication:
$$ p(s|c) = \prod_{i} p(s_i | s_{< i}, c), $$这里 $c$ 是一些条件 (可以是文本, 也可以是图像).
由 Transformer 预测出来的 tokens 收集起来经过 decoder $G$ 就可以得到’操作’过后的图像了. 当然了, Transformer 需要其它的方式训练. 现在这种方式已经被广泛应用于图像生成了 (如, Diffusion). 不过 Diffusion 里面采用 VQGAN 的流程主要是由于它的高效性.