Neural Discrete Representation Learning
预备知识
作者的目的是实现离散化的表示学习: 给定任意的模式, 编码成离散的表示.
既然本文是居于 VAE (变分自编码) 的框架实现的, 我们得对变分自编码有一个初步的了解. VAE 主要包含三个模块:
Encoder $\phi$: 它将输入 $x \in \mathbb{R}^D$ 映射到一个分布:
$$ q(z|x; \phi). $$比如当服从的高斯分布, 实质上 $\phi(x) \rightarrow (\mu, \sigma) \rightarrow \mathcal{N}(\mu, \sigma^2)$, 然后 $z$ 从该分布中采样即可;
Decoder $\Phi$: 它将隐变量 $z$ 映射回 (通常来说) $x$ 的空间:
$$ p(x|z; \Phi); $$还有一个先验分布 $p(z)$ 用于辅助训练.
VAE 的训练目标是极大似然的一个下界:
$$ \begin{align*} \log p(x) &= \log \int p(x, z) \mathrm{d}z \\ &= \log \int q(z|x; \phi) \cdot \frac{p(x, z)}{q(z|x; \phi)} \mathrm{d}z \\ &= \log \int q(z|x; \phi) \cdot \frac{p(x| z; \Phi) p(z)}{q(z|x; \phi)} \mathrm{d}z \\ &\ge \int q(z|x; \phi) \log \frac{p(x| z; \Phi) p(z)}{q(z|x; \phi)} \mathrm{d}z \\ &= \int q(z|x; \phi) \log \frac{p(z)}{q(z|x; \phi)} \mathrm{d}z + \int q(z|x; \phi) \log p(x|z; \Phi) \mathrm{d}z \\ &= \underbrace{-\mathbf{KL}(q_{\phi}\| p(z)) + \mathbb{E}_{z \sim q_{\phi}} \log p(x|z; \Phi)}_{\text{ELBO}}. \end{align*} $$ELBO 包括一个和先验分布的 KL 散度 (这部分通常是增加隐变量的 diversity 的), 以及一个正常的交叉熵 (如果 $p_{\Phi}$ 也是一个高斯, 则通常称之为重构损失).
核心思想
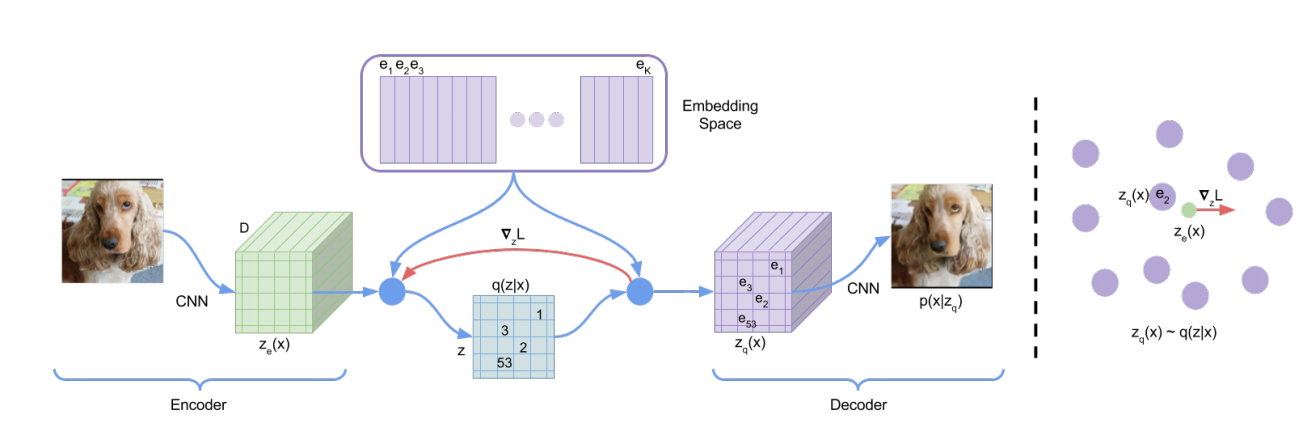
VQ-VAE 的希望 $z$ 不再局限于连续的向量, 而是离散的值, 做法其实极为简单:
预设一个 codebook $E \in \mathbb{R}^{K \times d}$;
给定一个输入 $x$, 其对应的离散值为
$$ x \rightarrow \phi(x) \rightarrow \text{argmin}_{k} \|\phi(x) - e_k\|, $$其中 $e_k$ 表示 codebook $E$ 中 $k$-th 行.
接下来, decoder 部分的输入将是 $e_{k^*}$ 而不再是 $z$ 了.
容易发现, 这其实相当于我们的后验分布为:
$$ q(z = e_{k^*}|x; \phi) = \left \{ \begin{array}{ll} 1 & k^* = \text{argmin}_{k} \|\phi(x) - e_k\|, \\ 0 & otherwise. \end{array} \right . $$但是这里其实有一个大问题, $\phi$ 的训练梯度来源:
- KL 散度, 但是上述的概率实际上的 ‘固定’ 的, 没法提供额外的信息;
- 交叉熵, 由于我们用 $e_{k^*}$ 替代了, 导致梯度没法直接计算.
对于第二点, 作者建议采取 straight-through estimator, 另外设计了另外两个损失用于训练 $\phi$ 以及 codebook $E$:
$$ L = \log p(x|z_q; \Phi) + \| \text{sg} (\phi(x)) - e_{k^*}\|_2^2 + \beta \cdot \| \phi(x) - \text{sg} (e_{k^*})\|_2^2. $$这里 $\text{sg}(\cdot)$ 表示 stop-gradient 操作, $\beta$ 是超参数 (默认为 0.25).
注: straight-through estimator (STE):
z_q = z + (z_q - z).detach()